Тема 3. Краткая характеристика статистических показателей

Основными параметрами выборки считаются средняя арифметическая и среднее квадратическое отклонение (сигма), так как большинство остальных показателей вычисляются на основе их числовых значений.

1. Средняя арифметическая (М), являясь основной характеристикой статистической совокупности (вариационного ряда), отражает уровень, по отношению к которому колеблются значения вариант в ней. Общая формула вычисления средней арифметической: , где М - средняя арифметическая; ∑х - сумма всех вариант ряда; N- объем выборки.

2. Среднее квадратическое отклонение (σ) есть мера варьирования признака в данной совокупности, т.е. величина колебания, вариант около их средней арифметической. Среднее квадратическое отклонение в квадрате называется дисперсией (σ²). Дисперсия вычисляется по формуле: 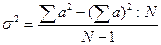, где сигма (σ) - среднее квадратическое отклонение; ∑ - знак суммирования; а - отклонения вариант от средней арифметической; М – средняя арифметическая; N - объем выборки.

3. Коэффициент вариации 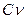. Как указывалось, среднее квадратическое отклонение характеризует степень отклонения вариант данной совокупности от среднего арифметического в абсолютных числах. Этого не достаточно для сравнения вариабельности двух или более совокупностей, так как величины сигмы не могут быть использованы, за исключением редкого случая, когда средние арифметические одинаковы или близки друг к другу. Для сравнения совокупностей по их вариабельности необходимо вычислить коэффициент вариации, который показывает, какой процент составляет сигма от средней арифметической и позволяет сравнить между собой по степени варьирования любые совокупности. Удобно коэффициент вариации вычислять по формуле: С 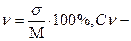коэффициент вариации; М - средняя арифметическая; σ - среднее квадратическое отклонение.

4. Ошибка средней арифметической (m_M) определяется по формуле: .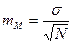

5. Показатель точности опыта (Р) выражает величину ошибки средней арифметической (в процентах) от самой средней арифметической и, таким образом, служит показателем точности определения последней. Чем больше показатель Р, тем меньше точность опыта. Показатель точности опыта часто вычисляется по формуле: 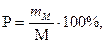или по формуле: 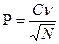, где Р – показатель точности опыта; М - средняя арифметическая; m_М – ошибка средней арифметической; 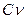- коэффициент вариации; N - объем выборки. Точность опыта считается удовлетворительной, если величина показателя (Р) не превышает 5%. Когда показатель точности опыта больше 5 % необходимо увеличить число наблюдений.

6. Критерий достоверности средней арифметической (t) вычисляется по формуле: 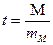. Средняя арифметическая считается достоверной, если t>3. Если t<3, то следует увеличить число наблюдений (вариант).

7. Медиана ( М_е)- это варианта, разделяющая вариационный ряд на две равные по числу вариант части. Порядковый номер медианной варианты в ранжированном вариационном ряду определяется по формуле: 0,5 (N+1), где N- объем выборки.

8. Мода (М_о) - точка на оси абсцисс, соответствующая максимальной частоте теоретической кривой распределения вариант. Этот показатель вычисляется в том случае, когда вариационный ряд разбит на классы, содержащие разное число частот. Приближенно за моду можно принять наиболее часто встречающуюся варианту ряда. Положение моды относительно средней арифметической взвешенного вариационного ряда определяет степень скошенности, или асимметрии кривой распределения ряда. В симметричном нормальном распределении мода совпадает со средней арифметической вариационного ряда. Вычисляется мода по формуле: 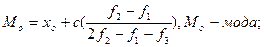х_о - начало модального класса, то есть меньшая граница того класса, который имеет наибольшую частоту; с - величина классового интервала; f₁ - частота класса, предшествующего модальному; f₂ - частота модального класса; f₃ - частота класса, следующего за модальным.

9. Коэффициент асимметрии (К_As) - мера отклонения распределения частот от симметричного их распределения относительно максимальной ординаты называется скошенностью, или асимметрией. Степень асимметрии вычисляется двумя способами.

Через разность между средней арифметической и модой и через отношение момента третьего порядка к кубу среднего квадратического отклонения.

Первый способ: 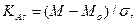где K_As - коэффициент асимметрии; М - средняя арифметическая; М_о - мода; 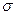- среднее квадратическое отклонение.

Отрицательное значение коэффициента асимметрии соответствует отрицательной асимметрии, положительное значение – положительной асимметрии. Иногда при измерении асимметрии вместо моды используется медиана. В этом случае коэффициент асимметрии измеряется по формуле:

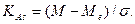
Второй способ: 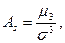или 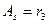, где A_s - показатель асимметрии;

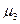- центральный момент третьего порядка; 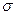- среднее квадратическое отклонение; 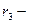основной момент третьего порядка. Показатель асимметрии может иметь как положительное, так и отрицательное значение. Ошибка показателя асимметрии вычисляется по формуле: 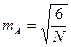, где m_А - ошибка показателя асимметрии; N - объем выборки.

10. Показатель эксцесса (E).

Степень отклонения эмпирической кривой распределения от нормальной теоретической кривой на своей вершине количественно выражается показателем эксцесса. Этот показатель определяется по формуле 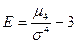или 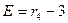, где Е – показатель эксцесса; 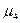- центральный момент четвертого порядка; 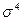- среднее квадратическое отклонение в четвертой степени; r₄- основной момент четвертого порядка.