Величин высоты растений А. высочайшего (A. altissima Swingle) в опыте (см)
| Границы классов | Середина класса (х) | Час-тота (f) | a | fa | fa2 | fa3 | fa4 | a+1 | (a+1)4 | (a+1)4f |
| 217-219,9 | 218,5 | -4 | -256 | -3 | ||||||
| 220-222,9 | 221,5 | -3 | -216 | -2 | ||||||
| 223-225,9 | 224,5 | -2 | -112 | -1 |
Продолжение табл.7
| 226-228,9 | 227,5 | -1 | -22 | |||||||
| 229-231,9 | 230,5 | |||||||||
| 232-234,9 | 233,5 | |||||||||
| 235-237,9 | 236,5 | |||||||||
| 238-240,9 | 239,5 | |||||||||
| C=3, А=230,5 | N=100 | К=8 | -60 | -498 |
Прежде чем переходить к вычислению условных моментов, проверим выполненные действия. Сумма чисел столбца 11 должна быть равна следующему выражению: 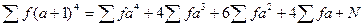
а) для контроля: 8152= 3420 +4 х 582 + 6 х 360 + 4 х 36 + 100 = 8152;
б) для опыта: 1638 = 2174 + 4(-498) + 6 х 266 + 4 (-60) + 100 = 1638.
Вычисляем условные моменты распределения (моментами распределения называют средние степени отклонений вариант от средней арифметической - это центральные моменты, а средние степени отклонений от произвольного числа называются условными моментами). Порядок момента равен степени, в которую возводится отклонение. Условные моменты вычисляются для получения возможности вычисления центральных моментов.
а) контроль:
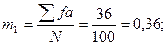
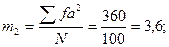
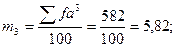
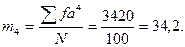
б) опыт:
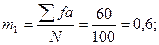
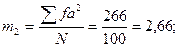
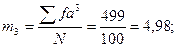
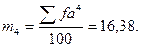
Вычисляем правую часть уравнений:
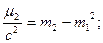
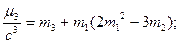
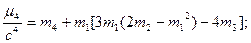
контроль:
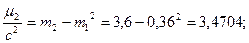
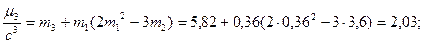
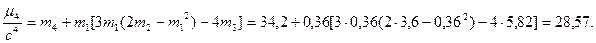 опыт:
опыт:
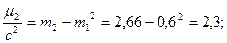
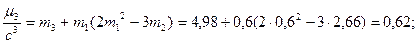
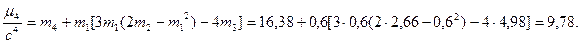 где
где 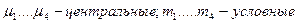 моменты.
моменты.
Проверку вычислений центральных моментов (деленных на степени классовых интервалов) покажем на контроле:
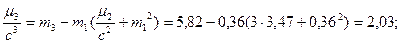
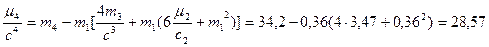
Как видим, значения центральных моментов, деленные на степени классового интервала, совпадают с вычисленными, следовательно, расчеты произведены верно. Аналогично проверяются вычисления и для опыта.
Находим центральные моменты из уравнений:
а) для контроля:
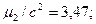
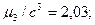
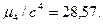
б) для опыта:
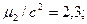
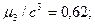
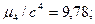
где с2 = 9; с3 = 27; с4= 81, с - классовый интервал, тогда для контроля: 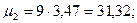
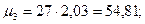
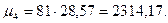
для опыта : 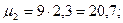
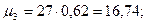
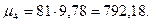
Вычисляем:
среднюю арифметическую (M= A+m1c.):
a) контроль: M=130,5+0,36 x 3 = 131,58;
б) опыт: М=230,5+0,6 х 3 = 232,3;
среднее квадратическое отклонение вычисляем по формуле 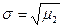 :
:
для контроля: 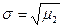 =
= 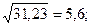
для опыта: 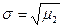 =
= 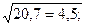
коэффициент асимметрии:
а) для контроля: 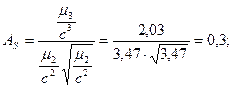
б) для опыта: 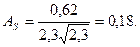
эксцесс: а) для контроля: 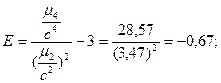
для опыта:Е=9,78 / (2,3)2 – 3 = - 1,15.
коэффициент вариации:
а) для контроля: 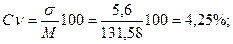
б) для опыта: 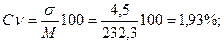
Дата добавления: 2020-10-25; просмотров: 730;











