Тема 6. Установление статистической достоверности различий между результатами опытов

Установление статистической достоверности различий между результатами опытов (вариантом и контролем, между различными вариантами опытов, средними арифметическими значениями) является наиболее распространенной, типичной задачей в экологии, биологии и опытном деле. Для этого, прежде всего, необходимо знать средние арифметические значения опытов, наблюдений, признаков, а также дисперсии или средние квадратические отклонения и ошибки средних арифметических. Приведем примеры определения статистической достоверности различий для малых и больших выборок.

1. Малые выборки (N₁<20, N₂<20).

Пример: сравнивались средние арифметические значения длины зрелых шишек у двух видов из рода ель- Picea Dietr. (ель сизая, или канадская - picea glauca (Moench) Voss. и ель колючая – p. pungens Engelm.). У p. glauca средняя длина шишек составляла М₁= 3,8 см, дисперсия - 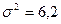, объем выборки - N₁ = 18; у p. pungens Engelm., соответственно, М₂ = 7,9 см; 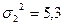, N₂= 18.

Сравнение дисперсий производится по формуле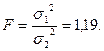

Для каждой из дисперсий находим число степеней свободы, которое равно объему выборки без единицы, то есть, для первого вида 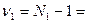18-1=17; для второго вида, соответственно,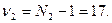

По таблице значений критерия F, для доверительного уровня Р = 95%, на пересечении столбца 17 и строки 17, т. е., в соответствии с числом степеней свободы 17 и 17, находим значение F = 2, 29, что больше вычисленного нами F =1,19, следовательно по размаху варьирования длины шишек два изучаемых вида достоверно не различаются.

В случае несущественно различающихся или равных дисперсий, как в нашем примере, средние арифметические значения сравниваются по формуле:

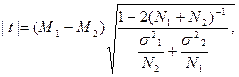
где t- критерий Стьюдента; M₁ и М₂ – сравниваемые средние арифметические, 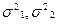- дисперсии сравниваемых выборок, N₁ и N₂ – их объемы. Подставляя в формулу значения, получаем 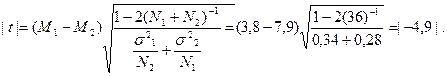Знак критерия не принимается во внимание. По таблице значений критерия Стьюдента, при числе степеней свободы 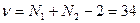и Р₁=0,95 t=2,030, что меньше вычисленного значения t = 4,9, следовательно, изучаемые два вида из рода ель достоверно различаются между собой по длине шишек.

Пример: сравнивались средние арифметические значения годичного прироста верхушечных побегов у растений двух видов в возрасте 9 лет из рода ель- Picea Dietr. (ель сизая, или канадская - picea glauca (Moench) Voss. и ель колючая – p. pungens Engelm.). У p. glauca средняя длина верхушечного побега составляла М₁= 14,6 см, дисперсия - 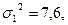, объем выборки - N₁ = 20; у p. pungens Engelm., соответственно, М₂ = 24,9 см; 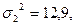, N₂= 20.

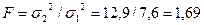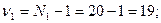
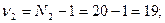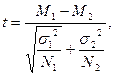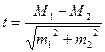Сравним дисперсии: . По справочной таблице при доверительном уровне Р₁= 95% и числах степеней свободы находим: F=1, 79. Следовательно, существенного различия по варьированию вариант у изучаемых видов не наблюдается. Разницу между средними арифметическими значениями, в т.ч. и когда дисперсии достоверно отличаются, можно оценить по формулам: или , c числом степеней свободы, определяемым по формуле: 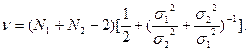Для решения, поставленной задачи необходимо определить и m_1, m₂:

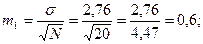
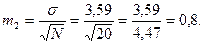Подставляя, имеющиеся значения в формулы получим: |t| =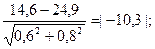 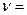35.

По справочной таблице, при доверительном уровне P₁= 95%, находим t=2,030, что меньше вычисленного критерия: 2,030 < 10, 3. Следовательно, между данными у изучаемых видов имеется достоверная разница по годичному приросту верхушечных побегов в девятилетнем возрасте.

2.Большие выборки (N₁> 20, N₂ > 20).

Сравнение средних величин производится по формуле (если объемы выборок незначительно различаются или равны): 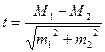, с числом степеней свободы: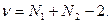

Рассмотрим пример вычисления критерия Стьюдента, по сравнению фенодаты начала разверзания почек у 100 видов древесных растений в Саратовской области и на полуострове Мангышлак, за одни и те же годы.

Получены следующие статистические показатели:

Саратовская область (М₁= 76, 9; 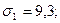N₁=100)

Полуостров Мангышлак (M₂=62,8; 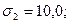N₂=100). Даты начала разверзания почек от первого марта ( М₁=76,9 = 16 мая; М₂= 62,8 = 2 мая).

Подставляя полученные значения в формулу, получим: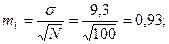

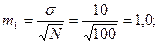
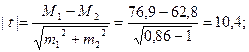
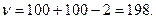
По таблице критерия Стьюдента, при ближайшем - меньшем числе степеней свободы 198, на 95% доверительном уровне t= 1,960, что меньше полученного нами значения. Следовательно, сравниваемые величины достоверно различимы. Установлено, что у древесных растений на полуострове Мангышлак почки разверзаются на 14 дней раньше, чем в Саратовской области.

При нормальном распределении вариант в больших вариационных рядах, сравнение средних значений можно осуществить без помощи таблиц и не прибегая к извлечению корней по формуле: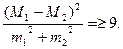

Если левая часть неравенства будет больше 9, то различия средних арифметических считается достоверным. Подставляем значения в формулу получим: 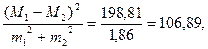что > 9.

Приведем пример установления статистической достоверности различий средних арифметических для ряда систематических признаков (морфология цветков, плодов и семян) у двух близких видов из рода Боярышник (Crataegus L.): 1- Crataegus ambigua C. A. M. - боярышник сомнительный и 2- C. transcaspica A.Pojark. –б. закаспийский. Исследования по систематике б. закаспийского были проведены в естественных, пустынных местообитаниях этого вида на полуострове Мангышлак. До семидесятых годов двадцатого столетия считалось, что популяция боярышника, произрастающая на полуострове Мангышлак, относится к европейскому виду- б. сомнительному. Были собраны семена в естественных местообитаниях боярышника, произрастающего на Мангышлаке (б. закаспийского) и б. сомнительного – в европейской части России. Из семян, в г. Шевченко - на полуострове Мангышлак, в экспериментальном ботаническом саду АН Казахстана, были выращены растения этих двух видов или, как считали некоторые систематики, представителей двух популяций одного вида. Растения содержались в идентичных условиях, что исключало влияние экологических факторов на формирование морфо-логических признаков или проявление фенотипической изменчивости. В результате у нас появилась возможность собрать информацию и провести статистическую обработку данных по морфологии плодов, семян, цветков, с целью установления видовой принадлежности особей боярышника, произрастающих на Мангышлаке. Цветки, плоды и семена изучали по методике, разработанной комиссией по семеноведению при Совете ботанических садов России. Полученный в ходе исследований материал был обработан методом вариационной статистики (Зайцев, 1984). Результаты исследований отражены в табл. 8.

Таблица 8