Пример синтеза корректирующего устройства в нелинейной системе
Выполним синтез корректирующего устройства в следящей системе со структурной схемой, изображенной на рис. 7.17. Система состоит из датчика рассогласований с передаточной функцией 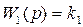 , безынерционного усилителя с нелинейной статической характеристикой с насыщением и коэффициентом передачи на линейном участке k2 (рис.1.5), двигателя с передаточной функцией
, безынерционного усилителя с нелинейной статической характеристикой с насыщением и коэффициентом передачи на линейном участке k2 (рис.1.5), двигателя с передаточной функцией 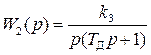 и редуктора с передаточной функцией
и редуктора с передаточной функцией 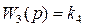 .
.

Рис. 7.17. Следящая система с редуктором
Зададимся значениями параметров: 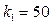 ;
; 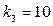 ;
; 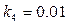 ;
; 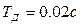 . Ошибка в системе при скорости
. Ошибка в системе при скорости 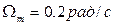 без учета момента нагрузки не должна превышать
без учета момента нагрузки не должна превышать 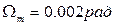 .
.
Требуется рассчитать линейное корректирующее устройство и определить коэффициент усиления усилителя k2 при работе на линейном участке статической характеристики.
Определим потребный коэффициент передачи разомкнутой системы (добротность по скорости)
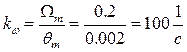 (7.31)
(7.31)
Запишем передаточную функцию для исходной разомкнутой системы при работе усилителя на линейном участке статической характеристики:
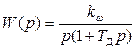 ,
,
где 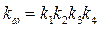 .
.
Для нелинейного звена со статической характеристикой с насыщением (рис. 7.18, а) гармоническая линеаризация дает
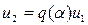 (7.32)
(7.32)

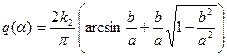 при
при 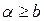
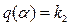 при
при 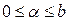 (7.33)
(7.33)
Перейдем к относительным амплитудам 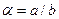 и выполним приведение нелинейности, отнеся коэффициент нелинейного звена
и выполним приведение нелинейности, отнеся коэффициент нелинейного звена 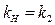 к линейной части системы. В результате получим значение коэффициента гармонической линеаризации для приведенной нелинейности:
к линейной части системы. В результате получим значение коэффициента гармонической линеаризации для приведенной нелинейности:
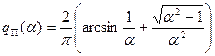 при
при 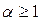
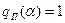 при
при 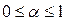
Примерный график изменения приведенного коэффициента гармонической линеаризации в зависимости от относительной амплитуды на входе нелинейности представлен на рис. 7.18,б.
Как видим, передаточная функция (7.31) является передаточной функцией приведенной линейной части, по которой строим располагаемую л. а. х. 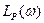 исходной линейной части (рис. 7.20) при учете значений
исходной линейной части (рис. 7.20) при учете значений 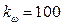 и
и 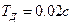 . Для этого через точку
. Для этого через точку 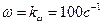 проводим линию с наклоном — 20 дб/дек. Участок этой линии до частоты
проводим линию с наклоном — 20 дб/дек. Участок этой линии до частоты 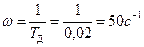 является первой асимптотой
является первой асимптотой 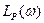 .
.
Вторую асимптоту в соответствии с передаточной функцией (7.31) проводим с наклоном — 40 дб/дек.


Рис. 7.18,а. Рис. 7.18,б. График
Характеристика изменения qп(α)
нелинейного звена
Выбираем тип желаемой л. а. х. 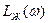 приведенной линейной части. Так как начальная асимптота располагаемой л. а. х. имеет наклон — 20 дб/дек, а конечная — наклон — 40 дб/дек, то в интересах простоты корректирующего устройства следует и качестве желаемой взять л. а. х. типа б (— 20, — 40, — 20, — 40 дб/дек).
приведенной линейной части. Так как начальная асимптота располагаемой л. а. х. имеет наклон — 20 дб/дек, а конечная — наклон — 40 дб/дек, то в интересах простоты корректирующего устройства следует и качестве желаемой взять л. а. х. типа б (— 20, — 40, — 20, — 40 дб/дек).
Поскольку задана только максимальная скорость слежения Ωm и не задано максимальное ускорение, это значит, что слежение происходит с медленным изменением скорости (при малых ускорениях). В этом случае не накладывается ограничений в области низких частот на выбор частоты ω1 первого излома желаемой л. а. х. Это дает возможность сразу выбрать протяженности участков h и h1 по h, 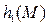 - кривым.
- кривым.
Зададимся реализуемым в скорректированной системе показателем колебательности 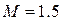 . За счет участка с наклоном — 20 дб/дек обеспечивается максимальный запас по фазе при частоте ωm и значении усиления по амплитуде
. За счет участка с наклоном — 20 дб/дек обеспечивается максимальный запас по фазе при частоте ωm и значении усиления по амплитуде
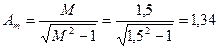
что при пересчете в децибелы дает
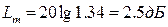
Проводим линию на уровне (штриховая линия на (рис. 7.19).Участок h желаемой л. а. х. должен делиться примерно пополам при пересечении этой линии.
Далее, пользуясь h, 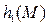 - кривыми (рис. 7.15), выбираем подходящий вариант для участков h и hl с тем, чтобы
- кривыми (рис. 7.15), выбираем подходящий вариант для участков h и hl с тем, чтобы
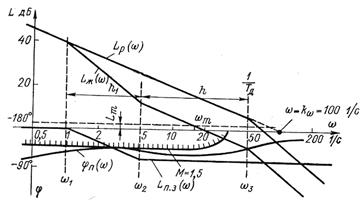
Рис. 7.19. Вариант желаемой л. а. х.
обеспечить показатель колебательности 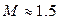 . Для обеспечения заданной точности первая асимптота желаемой л. а. х. должна совмещаться в низкочастотной области с первой асимптотой располагаемой л. а. х.
. Для обеспечения заданной точности первая асимптота желаемой л. а. х. должна совмещаться в низкочастотной области с первой асимптотой располагаемой л. а. х.
В интересах упрощения корректирующего устройства последняя асимптота желаемой л. а. х. должна либо совмещаться с последней асимптотой располагаемой л. а. х. в высокочастотной области, либо проходить параллельно ей.
На рис. 7.19 показан вариант желаемой л. а. х. с участками, соответствующими, согласно h, 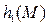 - кривым,
- кривым, 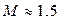 при протяженностях участков
при протяженностях участков
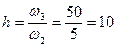
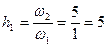
Вычитая из желаемой л. а. х. 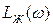 располагаемую л. а. х.
располагаемую л. а. х. 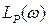 , получим л. а. х. линейного последовательного корректирующего устройства
, получим л. а. х. линейного последовательного корректирующего устройства 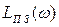 . Как видно, в качестве последовательного корректирующего устройства можно применить пассивный интегрирующий контур (рис. 7.20) с передаточной функцией
. Как видно, в качестве последовательного корректирующего устройства можно применить пассивный интегрирующий контур (рис. 7.20) с передаточной функцией
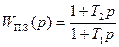 (7.34)
(7.34)
при 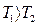
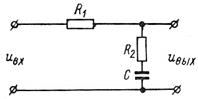
Рис. 7.20. Пассивный
интегрирующий контур
Постоянные времени контура определяются частотами излома 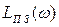 и связываются с величинами сопротивлений R1 и R2 и емкостью конденсатора С:
и связываются с величинами сопротивлений R1 и R2 и емкостью конденсатора С:

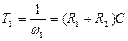
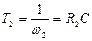 (7.35)
(7.35)
Корректирующее устройство обычно включается между каскадами усилителя. Если система работает на переменном токе, то перед корректирующим устройством включается демодулятор и фильтр, а после корректирующего устройства ставится модулятор. Поэтому при расчете параметров корректирующего устройства важно обеспечить согласование его с выходным сопротивлением цепей перед корректирующим устройством и входным сопротивлением последующих цепей. Это делается при расчете усилителя.
Для нашего случая имеем
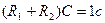

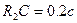
Можно задаться величиной емкости конденсатора, например 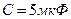 ; тогда из второго соотношения имеем
; тогда из второго соотношения имеем
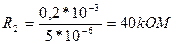
Из первого условия получим
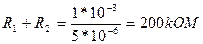
и, следовательно,
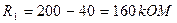
Поскольку корректирующее устройство не изменяет коэффициента передачи системы на низких частотах, то коэффициент усиления усилителя по напряжению для линейного участка статической характеристики определится из общего потребного коэффициента передачи:
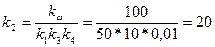
После выполнения синтеза корректирующего устройства целесообразно выполнить проверку. Для этого построим логарифмическую фазовую характеристику приведенной линейной части 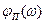 и запретную зону для нее при расчетном показателе колебательности
и запретную зону для нее при расчетном показателе колебательности 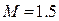 .
.
Запишем передаточную функцию приведенной линейной части скорректированной разомкнутой системы согласно (7.31) и (7.36):
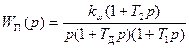 (7.36)
(7.36)
Соответствующая (7.36) частотная передаточная функция будет
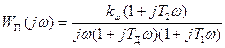 (7.37)
(7.37)
Согласно (7.36) логарифмическая фазовая характеристика приведенной линейной части определится соотношением
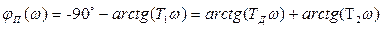 (7.38)
(7.38)
что с учетом значений постоянных времени дает
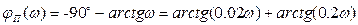 (7.39)
(7.39)
Результаты расчета по формуле (7.39) сведены в таблицу:
Таблица 7.1. Зависимость φп от частоты ω
| ω, 1/с | 0,5 | ||||||||
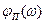 ,
град ,
град
| -111 | -125 | -134 | -129 | -122 | -123 | -140 | -156 | -167 |
По данным таблицы 7.1 на рис. 7.19 построена характеристика 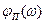 .
.
Учитывая изменение приведенного коэффициента гармонической линеаризации для нелинейной статической характеристики с насыщением 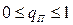 . заключаем, что запретная зона будет иметь максимальное значение запаса по фазе при всех частотах
. заключаем, что запретная зона будет иметь максимальное значение запаса по фазе при всех частотах 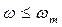 и составит согласно (7.11) величину
и составит согласно (7.11) величину
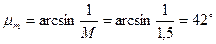
Остальная часть запретной зоны при 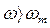 , строится с помощью окружности
, строится с помощью окружности 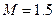 для приведенной линейной системы.
для приведенной линейной системы.
Из выполненного построения (рис. 7.19) видно, что потребный запас по фазе 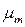 удовлетворяется точно при частотах участка h1 и удовлетворяется с запасом (как и следовало ожидать) при частотах участка h. В результате коррекции обеспечивается качество процесса в системе с
удовлетворяется точно при частотах участка h1 и удовлетворяется с запасом (как и следовало ожидать) при частотах участка h. В результате коррекции обеспечивается качество процесса в системе с 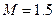 при запасе устойчивости по фазе
при запасе устойчивости по фазе 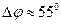 , что соответствует хорошему демпфированию нелинейной системы.
, что соответствует хорошему демпфированию нелинейной системы.
7.5. Контрольные вопросы к главе 7
1. Что принимается за значение показателя колебательности?
2. За счет чего происходят деформации запретных зон?
3. Какой график необходимо построить, чтобы определить показателя колебательности?
4. Что нужно определить, в первую очередь, при оценке показателя колебательности?
5. В каком порядке проводится синтез линейных корректирующих устройств?
6. Какого типа существуют желаемые л.а.х.?
7. Какой тип л.а.х. наиболее употребителен?
8. Какие требования накладываются на протяженность участков h и h1?
9. Какова связь между протяженностью участков h и h1 и показателем колебательности?
10. Какой подъем должна иметь логарифмическая амплитудная характеристика приведенной линейной части?
Литература
1. Баркин А. И. Оценки качества нелинейных систем/ А. И Баркин. – М.: Наука, 1982. – 357с
2. Белов Г. А. Теория автоматического управления (нелинейные и дискретные системы)/ Г. А. Белов. – Чебоксары.: Изд-во Чебоксарск. ун-та, 2009. – 447с
3. Теория автоматического управления. Часть 2/ Н.А. Бабаков,[и др.]; под общ. ред. А.А.Воронова. – М.: Высшая школа, 1986. – 504с.
4. Теория автоматического управления: учебник для вузов /С. Е. Душин, [и др.]; под общ. ред. В.Б.Яковлева. – М.: Высшая школа, 2003. – 567с.
5. Мирошник И.В. Теория автоматического управления. Нелинейные и оптимальные системы/ И.В. Мирошник. –СПБ.: Питер, 2004. – 272с.
6. Наумов Б. Н. Теория нелинейных автоматических систем/ Б.Н.Наумов. – М.: Наука, 1972. – 385с.
7. Бесекерский В.А. Теория систем автоматического регулирования / В.А. Бесекерский , Е.П. Попов. – М.: Наука, 2003. –747с.
8. Сборник задач по теории автоматического регулирования и управления / А. Н. Герасимов [и др.]; под общ. ред. В.А. Бесекерского. – 5-е изд., перераб. М.: Наука, 1978. – 512с.
9. Пальтов И.П. Нелинейные методы исследования автоматических систем/ И.П. Пальтов. – Л.: Энергия, 1976. – 128с.
10. Пальтов И.П. Качество процессов и синтез корректирующих устройств в нелинейных автоматических системах. И.П. Пальтов. – М.: Наука, 1975.– 368с.
11. Пантелеев А.В. Теория управления в примерах и задачах: учебное пособие/ А. В. Пантелеев, А.С. Бортаковский. – М.: Высшая школа, 2003. – 583с.
12. Попов Е.П. Теория нелинейных систем автоматического регулирования и управления/ Е.П. Попов. – М.: Наука, 1988. – 256с.
13. Хлыпало Е.И. Нелинейные системы автоматического регулирования/ Е. И. Хлыпало. – Л.: Энергия, 1967. – 452с.
Дата добавления: 2020-10-25; просмотров: 648;











