IV УСТРОЙСТВА ФИЛЬТРАЦИИ СИГНАЛОВ

Фильтры предназначены для того, чтобы из всех подаваемых на его вход сигналов пропускать на выход сигналы определенных, наперед заданных частот.

Фильтры классифицируются по тому, какова часть пропускаемого на выход частотного спектра исследуемого сигнала.

Фильтры нижних частот пропускают на выход все частоты, начиная с нулевой и до некоторой заданной частоты, называемой частотой среза f_ср. Для частот выше частот среза фильтры нижних частот ослабляют сигнал (рис.3.1, а). Диапазон частот от нуля до f_ср называют полосой пропускания.

Частота среза – это частота, при которой напряжение на выходе фильтра падает до уровня 0,707 от напряжения в полосе пропускания U_пр (т.е падает на 3 дБ). Диапазон частот, превышающий частоту f_в, называют полосой подавления (или заграждения). Это частота, при которой выходное напряжение на 3 дБ выше, чем выходное напряжение в полосе подавления. Интервал частот от f_ср до f_в называют переходным участком.

Фильтр верхних частот ослабляет все частоты, начиная от нуля и до f_ср, и пропускает все частоты выше f_ср до верхнего частотного предела используемой схемы ОУ (в идеале до бесконечности),(рис.3.1, б).

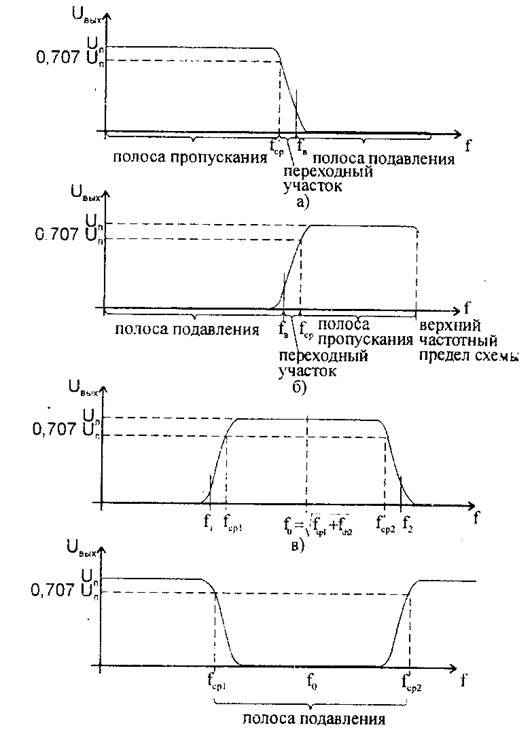
Рисунок 3.1 – Амплитудно частотные характеристики различных типов

Полосовой фильтр пропускает все частоты в полосе между нижней и верхней частотой среза f_ср1 и f_ср2. Все частоты ниже f_ср1 и f_ср2 подавляются (рис.3.1, в). Диапазоны от f₁` до f<sub>ср1</sub> и f<sub>ср2</sub> до f<sub>2</sub>` являются переходными участками. Геометрическое среднее частот f_ср1 и f_ср2 называют средней центральной частотой f₀ = 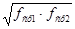. Режекторный полосовой фильтр (заграждения) ослабляет все частоты между f_ср1 и f_ср2 и пропускает все остальные частоты (рис.3.1, г). Эти фильтры используют чаще всего для подавления сигнала помехи, например сетевой помехи 50 Гц.

При расчете фильтров и изображений их частотных характеристик часто на практике используют логарифмические шкалы. Коэффициент усиления А в логарифмической шкале выражается в децибелах А(дБ) = 20·lgА, где А – числовое значение коэффициента усиления.

Шкала частот представляется в логарифмическом масштабе и использует два варианта разметки. Октавой называется изменение (увеличение или уменьшение) частоты вдвое. Например, если частота увеличивается от 500 до 1000 Гц, говорят, что она возрастает на одну октаву. Декадой называется десятикратное увеличение или уменьшение частоты. Так, если частота увеличивается от 100 до 1000 Гц, она возрастает на одну декаду. На (рис.3.2, а) показана частотная характеристика фильтра низких частот, имеющего скорость спада 6 дБ на октаву или 20 дБ на декаду.

Среди недостатков активных фильтров отмечают то, что они требуют наличия источников питания, а их рабочий диапазон ограничивается частотными свойствами ОУ.

Дадим основные определения, характеризующие основные параметры активных фильтров.

Полюсами фильтра с практической точки зрения называют слагаемые наклона его частотной характеристики на переходном участке, который обусловлен наличием RC – цепей, используемых для формирования частотных характеристик.

Порядок фильтра – это число его полюсов. Каждый полюс вносит в наклон переходного участка 6 дБ на октаву или 20 дБ на декаду. Число полюсов фильтра связывают также со степенью полиномов передаточных функций фильтров. Коэффициент затухания α определяет форму характеристики фильтра на переходном участке и вид выброса характеристики в полосе пропускания вблизи переходного процесса. Таким образом, коэффициент затухания определяет форму частотной характеристики фильтра, то есть его тип. На (рис.3.2, б) представлены частотные характеристики фильтров различных типов с различным коэффициентом затухания.

Неравномерность связывают с величиной отклонений (колебаний) вершины логарифмической амплитудно-частотной характеристики в полосе его пропускания (∆L).

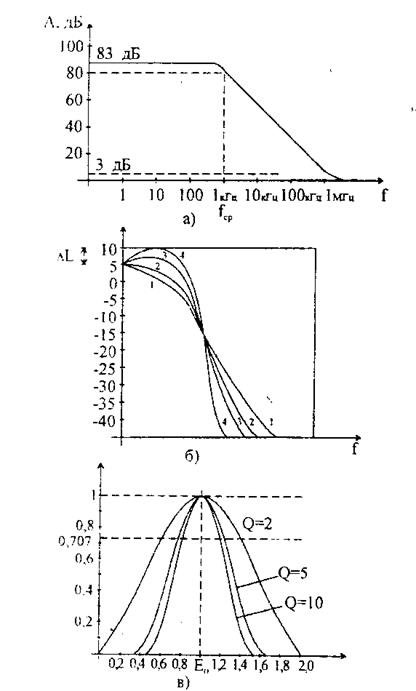
1 – фильтр Бесселя (α=1,732); 2- фильтр Баттерворта (α= 1,414); 3- фильтр Чебышева с неравномерностью 1 дБ; 4 – фильтр Чебышева с неравномерностью 3 дБ

Рисунок 3.2 – Основные характеристики фильтров различных типов

Добротность Q связывают среднюю частоту полосы пропускания и ее ширину на уровне 3 дБ. Рисунок (3.2 , в) иллюстрирует определение понятия «добротности». Численно добротность определяют как

Q = = ,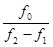

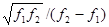где 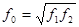- средняя частота, 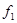и 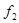- соответственно нижняя и верхняя частота среза на уровне 3 дБ от К_п в полосе пропускания.

Для активных фильтров Q = 1/α. Коэффициент усиления в полосе пропускания К_п активного фильтра определяют как К_п = U_вых/U_вх.

Допустимое отклонение от номиналов элементов или требуемого усиления для заданной схемы активного фильтра можно непосредственно связать с параметрами чувствительности схемы.

Чувствительность S определяется как выраженное в процентах изменение характеристики схемы при частичном изменении одной из независимых переменных в схеме. Чувствительность данного характеристического параметра, например избирательности Q активного фильтра относительно частичного изменения схемного параметра, определяется в следующем виде:

S ,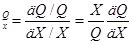

где X может быть любым из параметров пассивных элементов или усилителя.

Например, запись S_R1(ω₀) = - 0,5, где ω₀ = 2πf₀, а R₁ – сопротивление активного фильтра показывает, что ω₀ уменьшается на 0,5%, если R₁ увеличивается на 1%.

4.1 Основные схемы фильтров

Существует три наиболее популярных схемы фильтров, а именно фильтр Баттерворта (максимально плоская характеристика в полосе пропускания), фильтр Чебышева (наиболее крутой переход от полосы пропускания к полосе подавления) и фильтр Бесселя (максимально плоская характеристика времени запаздывания). Любой из этих типов фильтров можно реализовать с помощью различных вариантов схем для построения фильтров верхних и нижних частот, а также полосовых фильтров.

Фильтр Баттерворта обеспечивает наиболее плоскую характеристику

в полосе пропускания, что достигается ценой плавности характеристики в

переходной области, т.е. между полосами пропускания и задерживания.

Его амплитудно-частотная характеристика (АЧХ) задаётся следующей формулой:

U_вых/U_{в х}= ;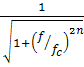

Где n – определяет порядок фильтра.

АЧХ в пределах полосы пропускания близка к равномерной. Поэтому этот фильтр используют тогда, когда желательно иметь постоянный коэффициент усиления для всех частот полосы пропускания. Фильтр Баттерворта дает нелинейную фазочастотную характеристику. Увеличение числа полюсов способствует повышению крутизны спада от полосы пропускания к полосе подавления. Однако выбор фильтра Баттерворта с целью обеспечения плоской характеристики, как правило, приводит к тому, что приходится поступаться всем остальным. Его характеристика идет горизонтально, начиная от нулевой частоты, перегиб ее начинается на частоте среза f_с , эта частота обычно соответствует точке минус 3 дБ.

В большинстве применений самым существенным обстоятельством

является то, что неравномерность характеристики в полосе пропускания не

должна превышать некоторой величины, скажем 1 дБ. Фильтр Чебышева

отвечает этому требованию, имея некоторую неравномерность характеристики по всей полосе пропускания, но при этом обеспечивает крутой спад АЧХ на границе полосы пропускания. Для фильтра Чебышева задают число полюсов и неравномерность в полосе пропускания. АЧХ этого фильтра описывается уравнением:

U_вых/U_{в х}= ;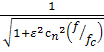

где c_n – полином Чебышева первого рода степени n, а ε – константа, определяющая неравномерность характеристики в полосе ее пропускания.

Фильтр Чебышева, как и фильтр Баттерворта имеет ФЧХ далекие от идеальных. На самом деле фильтр Баттерворта с максимально плоской

характеристикой в полосе пропускания не так привлекателен, как это может показаться, поскольку в любом случае приходится мириться с некоторой неравномерностью характеристики в полосе пропускания (для

фильтра Баттерворта это будет постепенное понижение характеристики при приближении к частоте f_с, а для фильтра Чебышева – пульсации, распределенные по всей полосе пропускания). Кроме того, активные фильтры, построенные из элементов, номиналы которых имеют некоторый допуск, будут обладать характеристикой, отличающейся от расчетной, а это значит, что в действительности на характеристике фильтра Баттерворта всегда будет иметь место некоторая неравномерность в полосе пропускания.

В свете вышеизложенного весьма рациональной структурой можно считать фильтр Чебышева. Иногда его называют равноволновым фильтром, так как его характеристика в области перехода имеет большую крутизну за счет того, что в полосе пропускания распределено несколько равновеликих пульсаций, число которых возрастает вместе с порядком фильтра. Даже при сравнительно малых пульсациях (порядка 0,1дБ ) фильтр Чебышева обеспечивает намного большую крутизну характеристики в переходной области, чем фильтр Баттерворта. Чтобы выразить эту разницу количественно, предположим, что требуется фильтр с неравномерностью характеристики в полосе пропускания не более 0,1 дБ и затуханием на частоте, отличающейся на 25 % от граничной частоты пропускания. Расчет показывает, что в этом случае требуется либо 19-полюсной фильтр Баттерворта, либо всего лишь 8-полюсный фильтр Чебышева.

Характеристика фильтра Чебышева имеет волнообразные зубцы в полосе пропускания и равномерна в полосе подавления. Количество зубцов в таких фильтрах тем больше, чем больше его порядок. Амплитуда этих зубцов может быть задана в процессе проектирования. Фильтр Чебышева обеспечивает на переходном участке крутые характеристики. Фазочастотная характеристика фильтра Чебышева еще более нелинейна, чем у фильтра Баттерворта. Наклон характеристики у фильтра Чебышева может превышать 6 дБ на октаву на один полюс. Зависимость ослабления в децибелах на переходном участке этого фильтра от частоты имеет вид:

где n – порядок фильтра, ω_ср = 2πf_ср, E – постоянная, принимающая значение от 0 до1 и характеризующая неравномерность характеристики в полосе пропускания.

Фильтры Бесселя обладают линейной фазовой характеристикой. Эти фильтры в отличие от фильтров Баттерворта и Чебышева практически не дают выбросов при подаче на вход ступенчатых сигналов, поэтому их применяют для фильтрации прямоугольных импульсов без изменения их формы. Фильтры Бесселя дают наклон меньший 6 дБ на октаву. Частота среза фильтра Бесселя определяется как частота, на которой запаздывание по фазе Θ равно половине запаздывания, максимально возможной для данного фильтра:

Θf_ср = Θ_max/2 = (nπ/2)/2рад,

где Θ – запаздывание по фазе.

OS = 20lgE + 6(n-1) + 20nlg(ω/ω_ср),