Оценка качества процессов в нелинейных системах по показателю колебательности

Поскольку запретные зоны для определения показателя ко­лебательности М в нелинейных системах строятся при учете всех возможных относителъных амплитуд α колебаний на входе нелинейности при всех возможных частотах, то оценка каче­ства процессов по показателю колебательности является такой же правомерной, как и в линейных системах. Приближенность оценки обусловливается приближенностью метода гармониче­ской линеаризации.

В нелинейных системах возможны в зависимости от значе­ний параметров системы и вида нелинейности области с равно­весно сходящимися процессами, области процессов, сходящихся к автоколебаниям, и области расходящихся процессов. При оценке качества процессов важно, прежде всего, определить указанные области. Кроме того, внутри области равновесно сходящихся процессов желательно оценить качество процессов
по показателю колебательности в зависимости от значений параметров.
По аналогии с линейными системами можно утверждать, что обеспечение любого значения показателя колебательности 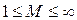соответствует устойчивому равновесно сходящемуся процессу с качеством, определяемым величиной М. Здесь остаются те же рекомендации к допустимым значениям показателя колебательности, т. е. 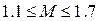; иногда .

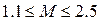Покажем, что при 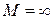запретные зоны вырождаются в линию—z(α), совпадающую с характеристикой 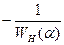, используемой для определения автоколебаний с помощью кри­терия Найквиста. Для этого, используя уравнение окружностей (7.6), образующих запретные зоны , будем полагать, что . Тогда для координат центра окружностей и ра­диуса получим

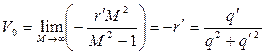
(7.12)

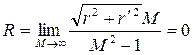
Сравнивая полученные выражения для U₀ и V₀ с формулой (7.4) характеристики 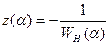, видим, что уравнениями (7.12) как раз определяется величина 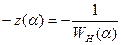в виде линии на комплексной плоскости.

Для линейных систем значению 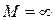соответствовала точка , т. е. линия 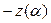в нелинейных системах есть обобщенный аналог точки линейных систем. Пересечение указанной линии с амплитудно-фазовой частотной характеристикой линейной части 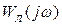соответствует периодическому режиму в системе (рис. 7.4).

Если же амплитудно-фазовая частотная харак­теристика линейной части 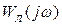не охватывает и не пересекает характери­стику 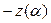, это значит, что в системе имеет место равновесно сходящийся про­цесс, качество которого оценивается по запретным зонам с .

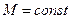Охват характеристики 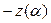характеристикой 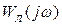без пересечения означает неустойчивость нелинейной системы, т. е. расходимость нелинейного процесса.

В результате одним несложным построением можно оце­нить появление всех возможных процессов в нелинейной системе

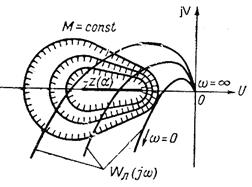
Рис. 7.4. Периодический

режим в системе

и качество равновесно сходящегося переходного процесса.

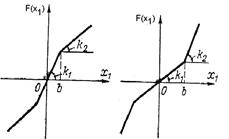
Оценим качество процессов в нелинейных системах с одно­значными статическими характеристиками. Вид запретных зон 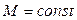для амплитудно-фазовых характеристик на ком­плексной плоскости или для логарифмических фазовых характеристик на логарифмической плоскости связан в этом случае с диапазоном изменения коэффициента гармонической линеари­зации 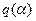. Согласно формулам для координат центра и ра­диуса окружностей, образующих запретные зоны, будем иметь различные запретные зоны (рис. 7.5, а, б), соответст­вующие диапазону изменения коэффициента гармонической ли­неаризации:

1 — при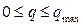

2 — при ;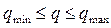

3 — при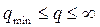

4 — при .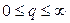

Каждому виду запретных зон соответствуют свои нелинейные однозначные нечетно-симметричные статические характери­стики.

Наиболее распространен случай 1, соответствующий, например, релейной характеристике с зоной нечувствительно­сти (рис. 1.3), характеристике с насыщением (рис. 1.5). Запретной зоне вида 2 соответствует характеристика с перемен­ным коэффициентом передачи (рис. 1.14).

а) б)

Рис. 7.5. Запретные зоны

Запретная зона вида 3 отвечает характеристике с переменным коэффициентом передачи, когда значение 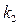велико, в пределе 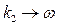. Запретная зона вида 4 соответствует идеальному релейному звену (рис. 1.13).

Выполним оценку качества процесса в системах с нелинейностями типа 1. Полагаем, что в результате структурных преобразований система приводится к свернутой структурной схеме, содержащей приведенную линейную часть и приведенную нелинейность (рис. 7.6). Приведение линейной части и нелиней­ности заключается в том, что из коэффициента гармонической линеаризации нелинейности выделяется множитель k_H, не зависящий от амплитуды гармонического сигнала, и передается в линейную часть ( 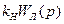). Величина k_H чаще берется такой, чтобы максимальное значение оставшегося приведенного коэффициента гармонической линеаризации равнялось единице. Для приведенного нелинейного звена коэффициент гармони­ческой линеаризации .

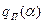Положим, что в качестве нелинейности имеем релейное звено с характеристикой, обладающей зоной нечувствительности (рис. 1.3).

Для такой характеристики коэффициент гармони­ческой линеаризации

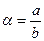
Рис. 7.6. Приведенная

структурная схема

Представляя коэффициент гармонической линеаризации в виде

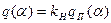(7.13)

где

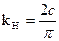
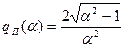(7.14)

приходим к схеме, изображенной на рис. 7.7.

Приведенный коэффициент гармонической линеаризации теперь изменяется в пределах 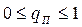, так как максимум функции

,

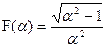входящей в (7.14), равен 0.5 при .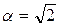

Такое представление системы удобно тем, что запретные зоны образуются окружностями с абсциссой центра и радиусом

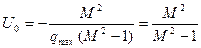
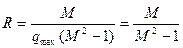
совпадающими с окружностями приведенной линейной системы (с исключенной приведенной нелинейностью), и касательными к этим окружностям, проведенными из начала координат (рис. 7.7). Это упрощает построение и позволяет сравнить ли­нейный вариант системы с нелинейным.

Приведенная характеристика

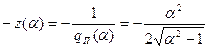
в данном случае будет двузначной.

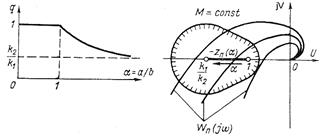
Из выполненного построения (рис. 7.7) следует, что в рас­сматриваемой релейной системе с линейной частью выше вто­рого порядка при малых значениях коэффициента передачи 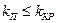имеет место устойчивый, равновесно сходящийся про­цесс. Качество процесса легко оценивается по запретной зоне 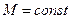, касательной к характеристике .

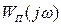При значениях 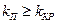, в системе с заданными па­раметрами имеется два периодических режима с одной частотой 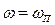и двумя значениями ампли­туд α_1п и α_2п. Периодиче­ские режимы для больших амплитуд 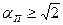, устой­чивы, т. е. соответствуют автоколебаниям. Периоди­ческие режимы при 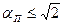соответствуют не­устойчивому предельному циклу. Прохождение ампли­тудно-фазовой частотной ха­рактеристики через точ­ку — 1, j0 для приведенной линейной системы

означает границу устойчивости, а для нелинейной системы — границу, отделяющую область равновесно сходящихся процессов от области автоколебаний. Следовательно, область автоколебаний в данной системе появляется за счет области

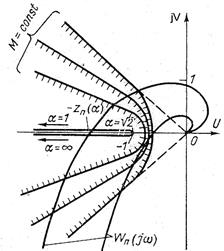
Рис. 7.7. Запретные зоны образованные

окружностями с абсциссой

центра U₀ и радиусом R

неустойчивости линейной системы и зна­чение коэффициента передачи, соответствующее границе устой­чивости, равно критическому значению коэффициента передачи нелинейной системы: .

Оценим процессы в нелинейной системе с нелинейным зве­ном, имеющим переменный коэффициент передачи (рис. 7.8, а, б).

Приближенно оценку ожидаемых процессов можно выполнить непосредственно по виду нелинейности, не вычисляя коэффи­циентов гармонической линеаризации.

Считаем опять систему состоящей из приведенной линейной части и приведенной нелинейности (рис. 7.6, а). Для первого случая (рис. 7.8, а), когда коэффициент усиления в системе

а) б)

Рис. 7.8. Нелинейная система с

переменным коэффициентом

передачи

снижается с возрастанием входной величины нелинейности, получим примерный вид графика изменения коэффициента гар­монической линеаризации q в зависимости от α (рис.7.9,а).

а) б)

Рис. 7.9. График изменения

коэффициента гар­монической

линеаризации

Здесь приведение заключается в передаче в линейную часть ко­эффициента k₁.

Характеристика 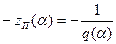в этом случае будет однозначной (рис. 7.9, б) и займет на отрицательной полуоси вещественный отрезок от - 1 до 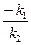при возрастании амплитуд α справа налево.

Запретные зоны 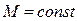образуются двумя окружностями и касательными к ним. Меньшая из окруж­ностей соответствует запретной зоне приведенной линейной системы, а вторая — определяется абсциссой центра

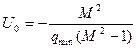
и радиуса

,

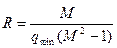где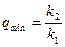

Если нанести на комплексную плоскость амплитудно-фа­зовые частотные характеристики приведенных линейных частей выше второго порядка (рис. 7.9, б), получим три области процес­сов. При малых коэффициентах передачи 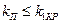это устойчи­вые, равновесно сходящиеся процессы с качеством, определяе­мым некоторым значением 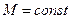. При значениях коэффициента передачи приведенной линейной части 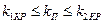в системе имеют место процессы, сходящиеся к автоколебаниям, частота и амплитуда которых определяется по точке пересече­ния характеристик 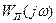и .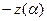

Для больших значений коэффициента передачи приведен­ной линейной части 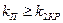характеристика 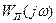охваты­вает характеристику 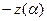и, значит, в системе имеем расходя­щиеся нелинейные процессы.

Таким образом, в зависимости от значения коэффициента передачи здесь имеем три области: область устойчивости равно­весия, область автоколебаний и область неустойчивости, причем область автоколебаний занимает часть области неустойчивости приведенной линейной системы.

Оценим процессы в нелинейной системе, когда коэффициент передачи нелинейного звена возрастает с увеличением входной величины х₁(рис. 7.8, б). Здесь при приведении нелинейности целесообразно сохранить 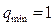, т. е. отнести к линейной части коэффициент . Коэффициент передачи приведен­ной линейной части k_л при малых отклонениях 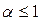оста­нется таким же, как и в предыдущем случае.

Приведенный коэффициент гармонической линеаризации с учетом принятого условия изобразится в виде графика q(α) (рис. 7.10, а) и будет изменяться в пределах

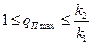
Тогда характеристика 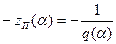займет отрезок на оси вещественных от 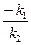до — 1 (рис. 7.10, б). Возрастание амплитуд вдоль этого отрезка происходит слева направо. Это значит, что при пересечении характеристик 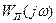и 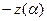получим неустойчивое периодическое решение.

Запретные зоны 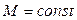здесь образуются большой ок­ружностью, соответствующей приведенной линейной системе, и малой — соответствующей .

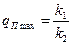а) б)

Рис. 7.10. Оценка процессов в нелинейной

системе

Построив амплитудно-фазовые частотные характеристики для приведенной линейной части 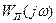при различных коэф­фициентах передачи 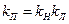, можно сделать заключение о процессах в системе.

Как видим, при малых коэффициентах передачи 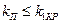имеем равновесно сходящиеся процессы. При значениях 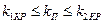получим неустойчивые периодические ре­жимы, т. е. устойчивость в малом и неустойчивость в большом. Для больших значений коэффициента передачи линейной части 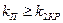имеем неустойчивость в целом.

Область неустойчивых предельных циклов практически можно отнести к области неустойчивости, так как всегда най­дутся начальные значения отклонений в системе, выходящие за предельный цикл. Указанная область, как видно из рис. 7.10,б, появилась за счет сужения области устойчивости приведенной линейной системы. Здесь граничный коэффициент линейной системы , а практическая неустойчивость нелиней­ной системы начинается при .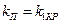

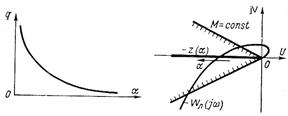
Рассмотрим систему с идеальным релейным звеном. Для такого звена имеем коэффициент гармонической линеаризации

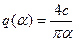
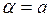
Коэффициент гармонической линеаризации изменяется в пределах 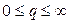(рис. 7.11, а). Характеристика 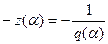занимает всю полуось вещественных от 0 до - ∞ (рис. 7.11, б) при возрастании амплитуд справа налево вдоль характеристики.

Следовательно, при линейной части выше вто­рого порядка получим режим автоколебаний, определяемый точкой

а) б)

Рис. 7.11. Изменение коэффициента

гармонической линеаризации

пересечения характеристик и .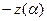

Аналогично выполняется оценка качества процессов и при наличии в системе двузначных статических нелинейностей, а также динамических нелинейностей. Правда, несколько услож­няется процесс построения запретных зон .