Процессы управления, сопровождающиеся вынужденными вибрациями

Рассмотрим случай, когда в системе протекает некоторый процесс управления, а кроме того к системе приложено внешнее периодическое воздействие. Уравнение динамики системы (рис. 6.1) в этом случае получит вид

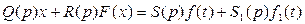
где 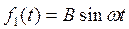, a f(t) — медленное по сравнению с f₁(t) воздействие, т. е. спектр возможных частот изменения f(t) много меньше ω. Решение будем искать в виде

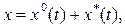(6.9)

где ;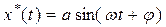

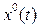—тоже медленная по сравнению с 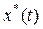функ­ция времени, определяющая процесс управления при на­ложенных на него вынужденных вибрациях .

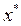Полагая, что основной процесс управления 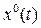про­текает настолько медленно, что за один период колеба­ний 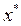можно приблизительно считать величину 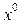неиз­менной, используем прежние формулы гармонической линеаризации (4.15), а именно

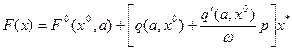(6.10)

где F⁰, q и q' вычисляются по формулам (4.16) и (4.17). Для некоторых конкретных нелинейностей эти функции приведены в разделе 4.2 (примеры 6—10).

Подставив (6.10) и (6.9) в уравнение (6.8), разобьем его на два. Для медленных составляющих (процесс уп­равления) имеем

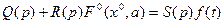(6.11)

а для вибрационных составляющих

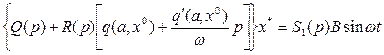(6.12)

Неизвестные 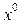и α могут быть определены только на основе совместного решения обоих уравнений. Если, решив уравнение (6.12), найти зави­симость 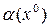и подставить ее в выражение 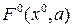, полученное по формуле (4.17), то найдем новую нели­нейную функцию

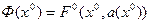(6.13)

Тогда уравнение для процесса управления (6.11) при­мет вид

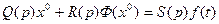(6.14)

Нелинейная функция 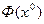облада­ет тем свойством, что она имеет вид плавной кривой (рис. 6.8) для любых нелинейностей F(x), в том числе релейных и гистерезисных. Поэтому эту функцию можно линеаризовать обычным порядком, определив крутизну в начале координат (рис. 6.8):

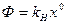
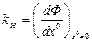(6.15)

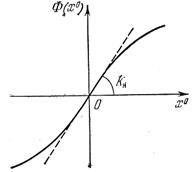
Рис. 6.8. Линеаризация

функции

Но согласно (6.13) имеем

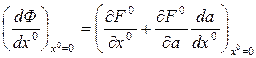(6.16)

а согласно (4.17)

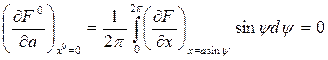(6.17)

так как произведение четной функции на нечетную ин­тегрируется за период. В соответствии с этим вместо (6.15) получаем важный результат:

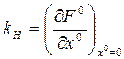(6.18)

Это значит, что для определе­ния k_H не нужно находить за­висимости 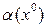и строить но­вую нелинейную функцию 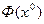, а достаточно взять част­ную производную по 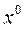от име­ющегося для каждой нелиней­ности выражения 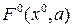. С заменой (6.15) уравнение для процесса управления (6.14) принимает вид линейного уравнения

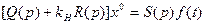(6.19)

где 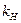— коэффициент усиления нелинейности в процессе управления, определяемый по формуле (6.18). Например, для идеальной релейной характеристики (см. раздел 4.2):

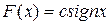
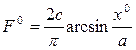
Получим

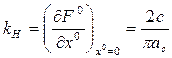(6.20)

где α_с — амплитуда симметричных вынужденных колеба­ний в данной системе, найденных согласно раздела 6.1.

Для релейных характеристик с зоной нечувствитель­ности и с петлей, дифференцируя (4.31), находим

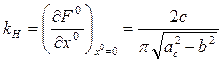(6.21)

Рис.6.9. Зависимость Рис.6.10.Зависимость

коэффициента k_H от коэффициента k_H

амплитуды симметричных для релейной

вынужденных колебаний характеристики

На рис. 6.9 представлена зависимость коэффициента 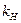от амплитуды симметричных вынужденных колебаний.

Аналогично для релейной характеристики общего вида (рис. 6.10) получаем

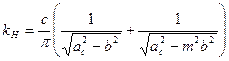(6.22)

Для кусочно-линейной характеристики с зоной не­чувствительности (рис. 6.11) имеем

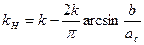(6.23)

а для характеристики с насыщением (рис. 6.12)

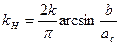
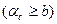(6.24)

Итак, пользуясь значениями коэффициента усиления 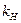, мы можем определять процесс управления в нелиней­ной системе по линейному уравнению (6.19) на базе линейной теории. Однако при этом надо учитывать, что коэффициент 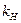имеет необычные свойства. В самом де­ле, как видно из формул (6.20) — (6.24), он зависит от амплитуды симметричных вынужденных колебаний α_с.

Рис.6.11. 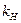для Рис.6.12. 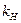для

характеристики с зоной характеристики

не­чувствительности с насыщением

Эта амплитуда в свою очередь, согласно раздела 6.1, зависит от структуры и параметров линейной части системы (k_i, T_i) и еще, что очень важно, от амплитуды В и частоты и внешнего вибрационного воздействия. Поэтому при синтезе системы (6.19), т. е. при выборе ее структуры и параметров надо знать зависимость

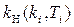, (6.25)

а зная (или выбирая) внешнее вибрационное воздейст­вие, надо учитывать также зависимость

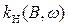(6.26)

Итак, процесс управления при наложенных на него вынужденных вибрациях исследуется по линейному уравнению (6.19) без определения зависимости 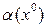. Однако, если все же необходимо определить величину амплитуды 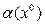, то аналогично уравнению (6.5) реше­ние уравнения (6.12) запишется в виде

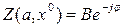
где

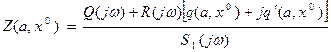
Графическое решение получается, как показано на рис. 6.2, с той только разницей, что здесь строится се­рия кривых Z(α) для разных значений 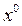. В результате на пересечениях этих кривых с окружностью радиуса В и определяется искомая зависимость 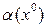. Тогда можно, согласно (6.15), найти и нелинейную функцию 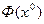, если необходимо учесть эту нелинейность в урав­нении процесса управления (6.16).

В связи с изложенным, на практике часто возникают следующие две важные частные задачи.

1. Вибрационное сглаживание и вибрацион­ная линеаризация нелинейности при помощи вынужден­ных вибраций.Свойство плавности функции 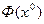(рис. 6.8) как характеристики прохождения медленного сигнала в процессе управления 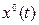через нелинейное звено при любом очертании нелинейности F(х), имею­щей скачки и петли, называется вибрационным сглажи­ванием нелинейности для процесса управления при на­личии вынужденных вибраций. Поскольку за счет этого возникает возможность обычной линеаризации получен­ной сглаженной характеристики (рис. 6.8) в виде 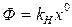, то говорят также о вибрационной линеаризации нелинейности.

В технике вибрационное сглаживание применяют следующим образом.

Пример 6.2. Непосредственно у входа нелиней­ного звена (например, релейного элемента), как показа­но на рис. 6.13, прикладывается внешнее вибрацион­ное воздействие 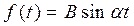с частотой выше полосы пропускания линейного звена 2. Тогда вынужденные вибрации локализуются во внутренней части системы.

Сигнал на входе нелинейности имеет вид

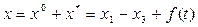
Причем

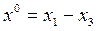
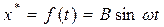
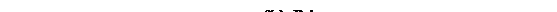
Рис. 6.13. Система с внешним вибрацион­ном

воздействием

Отсюда следует, что амплитуда α_с и фаза φ симметрич­ных вынужденных вибраций переменной х равны соот­ветственно , .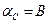

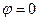Таким образом можно ликвидировать гистерезисную петлю или зону нечувствительности реле (рис. 6.9) и получить для сигнала управления, согласно (6.21), ли­нейную характеристику с коэффициентом

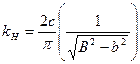при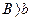

или же ликвидировать зону нечувствительности (рис. 6.11), получив

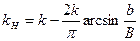при B > b

Аналогично можно преобразовать сухое трение в трение, пропорциональное скорости, и т. п.

Величину 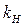можно регулировать амплитудой В внешнего воздействия, не выводя ее, конечно, за допу­стимые пределы. Кроме того, амплитуда В должна быть во всяком случае больше максимально возможного значе­ния сигнала 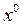, до которого хотят обеспечить линей­ность характеристики. Например, для петлевой релейной характеристики (рис. 6.9), согласно (4.31), должно быть .

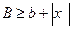2. Вибрационная помехоустойчивость нели­нейной системы управления. Пусть в уравнении нели­нейной системы (6.8) 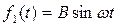представляет внешнюю вибрационную помеху (например, со стороны изгибных вибраций корпуса летательного аппарата, вос­принимаемых гироскопом вместе с полезным сигналом по углу тангажа). Характеристическое уравнение систе­мы для полезного сигнала в процессе управления, согласно (6.19), имеет вид

,

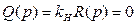где коэффициент 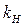зависит (6.26) от амплитуды В и частоты ω внешней вибрационной помехи. Следо­вательно, от этих параметров помехи будет зависеть ка­чество процесса управления и даже устойчивость системы.

Таким образом, если устойчивость чисто линейной системы, как мы знаем, не зависит от внешнего воз­действия, то в нелинейной системе устойчивость может от него зависеть. Предельное значение амплитуды виб­рационной помехи В, до которой система остается еще устойчивой, называется границей вибрационной помехо­устойчивости системы.

Пример 6.3. Определим вибрационную поме­хоустойчивость самолета с автопилотом. Схема системы изображена на рис. 6.14, а, где 1 — измерители, 2,4 — привод с обратной связью, 3 — корпус самолета.

Рис. 6.14. Схема системы самолета

с автопилотом

Уравне­ние углового движения самолета по тангажу

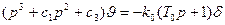
где 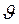— отклонение самолета по тангажу, δ — отклоне­ние руля.

Уравнение измерителей

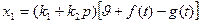
где 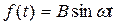— вибрационная помеха (например, измерение гироскопом изгибных вибрации корпуса самолета),

g(t)— медленное управляющее воздействие.
Уравнение привода руля

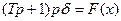(6.27)

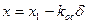
где F(x) — нелинейное ограничение скорости привода (рис.1.5).

Если 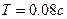, а частота вибрации 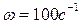, амплитуда вынужденных вибраций на выходе привода руля будет ослаблена в 800 раз. Поэтому можно счи­тать, что вибрации туда не проходят. Следовательно, амплитуду симметричных вынужденных колебаний на входе нелинейности х можно вычислить по формуле

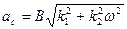
и для данной нелинейности (рис. 6.14,б), согласно (6.24), получаем

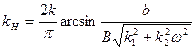(6.28)

Уравнение привода руля для процесса управления вместо (6.27) примет вид

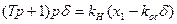
Характеристическое уравнение всей системы для процесса управления будет иметь пятую степень:

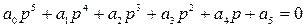
Предпоследний определитель Гурвица

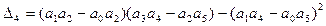
при некоторых числовых значениях параметров системы принимает вид

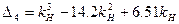
График зависимости 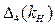изображен на рис. 6.15,а. Условие устойчивости 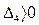выполняется при 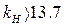. Легко проверить, что при этом положительны и остальные определители Гурвица: их положительность сводится к положительности всех коэффициентов урав­нения и неравенству

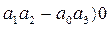
Из формулы (6.28) находим максимально допустимую амплитуду внешней вибрационной помехи по условию устойчивости 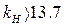в виде

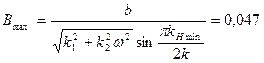
где , , , , , .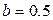

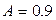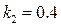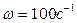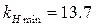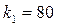Если при этом расчете системы надо выбрать, напри­мер, наилучший коэффициент обратной связи привода 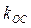то указанные вычисления надо провести для разных значений 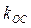, определяя каждый раз граничную величи­ну 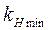. Результаты такого расчета приведены в виде графика на рис. 6.15, б. Этот график дает границу по­мехоустойчивости системы по коэффициенту 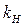, которую по вышеописанной формуле легко пересчитать на до­пустимую амплитуду B_max внешней вибрационной помехи.

Рис.6.15,а.Зависимость Рис.6.15,б. Граница

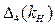по­мехоустойчивости

системы