Синтез линейных корректирующих устройств в нелинейных системах

Метод синтеза корректирующих устройств в нелинейных системах по показателю колебательности М базируется на той же основе, что и метод синтеза корректирующих устройств в линейных системах. Качество процесса в системе связывается с вы­бранной величиной показателя колебательности 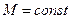, реализуемого в системе.

Если для исходной нелинейной системы построить запретную зону для выбранного значения 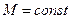и амплитудно-фазо­вую частотную характеристику линейной части , то с по­мощью линейной коррекции следует так деформировать харак­теристику , чтобы ее вывести из запретной зоны (рис. 7.12, а). Аналогично для логарифмических характе­ристик следует деформировать логарифмическую фазовую ха­рактеристику (л. ф. х.) линейной части так, чтобы вывести ее из запретной зоны 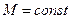(рис. 7.12, б).

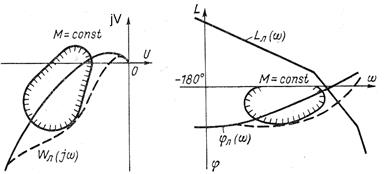
а) б)

Рис. 7.12. Деформирование л. а. х. и л. ф. х.

Синтез линейных корректирующих устройств выполняется с помощью логарифмических характеристик и включает в себя нижеследующие этапы.

1. Построение располагаемой логарифмической амплитуд­ной характеристики (л. а. х.) приведенной линейной части. Рас­полагаемая л. а. х. строится по исходной структурной схеме системы.

2. Построение желаемой л. а. х. приведенной линейной части системы. Желаемая л. а. х. строится по заданным требо­ваниям на проектирование и выбранному показателю колеба­тельности М. Как исходная линейная часть, так и линейная часть скорректированной системы считаются минимально-фа­зовыми (состоящими из устойчивых звеньев). Это обеспечивает однозначное соответствие друг другу л. а. х. и л. ф. х., и синтез выполняется только по логарифмическим амплитудным характе­ристикам.

3. Определение л. а. х. последовательного корректирую­щего устройства. Л. а. х. последовательного корректирующего звена получается вычитанием из л. а. х. желаемой л. а. х. рас­полагаемой:

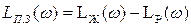
4. Реализация коррекции. Под реализацией коррекции понимается определение схемы корректирующего устройства и расчет ее элементов. Если оказывается целесообразным вместо последовательной коррекции применение параллельного кор­ректирующего устройства или обратной связи, то выполняется пересчет последовательного корректирующего устройства по формулам или таблицам эквивалентного перехода, имеющимся в литературе.

5.Проверка результата выполненного синтеза. В проверку входит построение запретной зоны 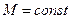для л. ф. х. при­веденной линейной части и построение самой л. ф. х. скорректи­рованной системы.

Наибольшую сложность при синтезе корректирующих устройств составляет определение желаемой л. а. х.

При синтезе линейных статических систем и систем с астатизмом первого порядка рекомендуемыми желаемыми л. а. х. являются л. а. х. типов а, б, в, г (рис. 7.13). Указанные л. а. х. являются желаемыми и для линейных частей нелинейных систем.

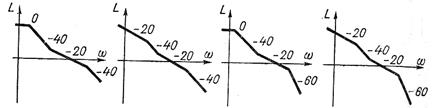
а) б) в) г)

Рис. 7.13. Желаемые л. а. х.

Рассмотрим наиболее употребительную л. а. х. типа б и за­претную зону 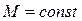для широко распространенных л.а.х.(рис.7.14), когда коэффициент гармонической линеаризации изменяется в пределах 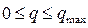. На рис. 7.14 также изображена штриховой линией запретная зона 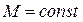для л. ф. х. приведенной линейной системы.

В линейных системах требуемый запас по фазе обеспечивался за счет достаточной протяженности асимптоты л. а. х. с наклоном — 20 дб/дек в окрестности частоты среза 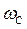. При этом, на протяженность асимптоты с наклоном — 40 дб/дек

никаких ограничений не накладывалось. Здесь введены относительные частоты, где 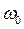— значение частоты при

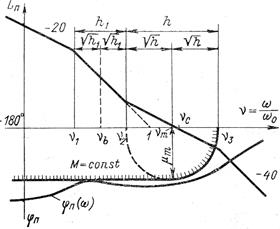
Рис. 7.14. Наиболее употребительная

л. а. х. типа б

пересечении оси частот продолжением второй асимп­тоты л. а. х.

В нелинейной системе, как видно на рис. 7.14, следует не только обеспечить достаточную протяженность участка h, но и наложить ограничение на протяженность участка h₁.

Найдем связь между протяженностями участков h и h₁ и показателем колебательности 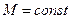из условия незахождения л. ф. х. приведенной линейной части 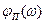в запретную зону.

Нормированное значение передаточной функции для л. а. х. будет

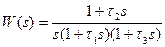, (7.15)

где 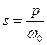— новое значение оператора;

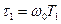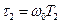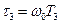, , — относительные постоянные времени.

Протяженность участка л. а. х. с наклоном — 20 дб/дек:

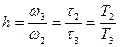(7.16)

протяженность участка л. а. х. с наклоном — 40 дб/дек:

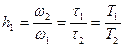(7.17)

С учетом (7.16) и (7.17) нормированную передаточную функ­цию (7.15)запишем в виде

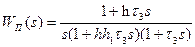, ( 7.18)

а соответствующая ей нормированная частотная передаточная функция при 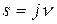будет

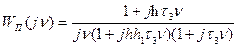(7.19)

Согласно (7.19) л. ф. х. приведенной линейной части системы определится соотношением

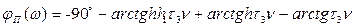
откуда запас по фазе, соответствующий желаемой л. а. х. типа б, будет

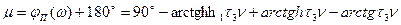(7.20)

При достаточной протяженности участков h и h₁ желаемой л. а. х. в приведенной линейной части для частот, близких к ча­стоте среза, разность

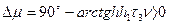
будет величиной сравнительно малой.

При этом для определения протяженности участка h можно воспользоваться приближенным соотношением, получаемым из (7.20) без учета значения 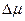, т. е.

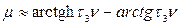(7.21)

Согласно (7.21) выражение для запаса по фазе можно за­писать в виде

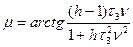(7.22)

Исследуя последнее выражение на максимум, получим

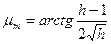(7.23)

при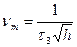

Это максимальный запас по фазе, обеспечиваемый за счет протяженности участка h.

Необходимый максимальный запас по фазе, определяемый за­претной зоной, согласно (7.11), составляет

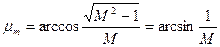
или

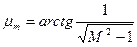(7.24)

Приравняв тангенсы для μ_m из (7.23) и (7.24), получим

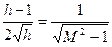
Откуда

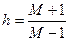
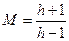(7.25)

Поскольку максимальные имеющийся и необходимый за­пасы по фазе приравнивались при частоте 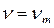, то участок л. а. х. с наклоном — 20 дб/дек следует располагать по возмож­ности симметрично относительно частоты 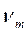. Деление участка h пополам относительно частоты 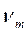в логарифмическом масштабе (рис. 7.14) в обычном масштабе частот означает, что

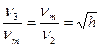
Для определения протяженности участка h₁ используем точную формулу для запаса по фазе (7.20). Потребуем, чтобы запас по фазе при частоте 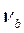соответствующей середине участка h₁ составлял величину 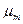. Тогда, согласно (7.20), получим

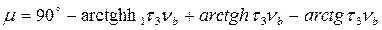
или

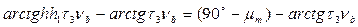
Взяв тангенсы разностей углов, соответствующих левой и правой частям последнего равенства, получим

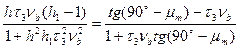(7.26)

Подставляя в (7.26) значение

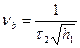
и учитывая, что

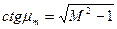
имеем

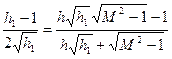
Разрешая последнее равенство, относительно h и учитывая (7.25), окончательно получим

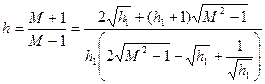(7.27)

Полученная формула (7.27) связывает значения протяженностей участков h и h₁ с показателем колебательности М для желаемой л. а. х. приведенной линейной части типа б. Анало­гично получаются и формулы, связывающие протяженности участков h и h₁ с показателем колебательности М для других типовых желаемых л. а. х.:

для л. а. х. типа а:

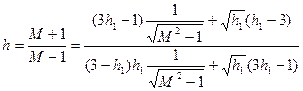(7.28)

для л. а. х. типа б:

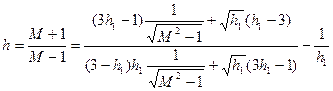(7.29)

для л. а. х. типа г:

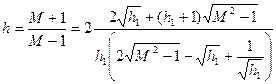(7.30)

Во всех приведенных формулах протяженность участка h выбирается исходя из одного и того же приближенного условия. Для характеристик а и б, как было показано при выводе фор­мулы для л. а. х. б, это условие обеспечивает избыток по фазе в окрестности частоты среза 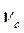и близкой к ней частоте 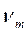. В слу­чае характеристик в и г, когда последняя асимптота имеет на­клон — 60 дб/дек, возможен и некоторый недостаток в запасе по фазе в окрестности частоты среза. При выборе протяженно­сти участка h₁ обеспечивается нужный запас по фазе (без избытка и недостатка) при частоте .

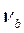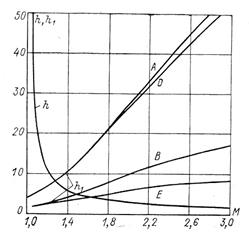
Рис. 7.15. h, 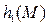– кривые

На рис. 7.15 представлены кривые, построенные по форму­лам (7.27-7.30), которые будем называть h, 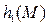- кривыми. Используя h, 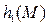- кривые, можно по задан­ному показателю колебательности 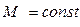определить по­требные протяженности участков h, и h₁ и, следовательно, от­носительные частоты 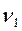, , 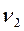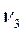или абсолютные частоты ω₁, ω₂, ω₃.

С помощью полученных h, 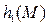-кривых определение же­лаемых л. а. х. линейной части может выполняться без всяких расчетов. При этом не обязательно выбирать h и h₁ соответст­вующими одному значению 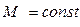. Часто возможны слу­чаи, когда в интересах простоты корректирующих средств при­ходится при выборе протяженности участка h принимать зна­чение показателя колебательности M₁, а для участка h₁ — не­которое значение M₂ (обычно 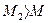). Тогда реализуемый в системе показатель колебательности будет заключен в неко­торых пределах 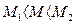. Уточнение реализуемого значе­ния М легко выполнить построением запретной зоны 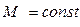и логарифмической фазовой характеристики приведенной ли­нейной части скорректированной системы.

Кроме требований, накладываемых на протяженность участ­ков h и h₁, необходимо определить подъем желаемой л. а. х. приведенной линейной части системы, исходя из заданной точ­ности. Оценка точности нелинейных систем и определение подъема желаемой л. а. х. связаны с видом статической нели­нейности вблизи нуля.

Если статические характеристики вблизи нуля аппроксими­руются линейным участком (рис. 7.16, а), то нелинейные системы к концу переходного процесса могут рассматриваться как ли­нейные. Подъем желаемой л. а. х. в этом случае определяется, как в линейных системах, по общему коэффициенту передачи 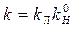. Причем 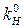определяется, как тангенс угла наклона касательной или секущей нелинейной характеристики вблизи нуля (рис. 7.16, а).

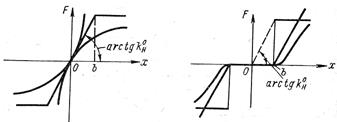
а) б)

Рис. 7.16. Определение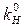

Логарифмическая амплитудная характери­стика приведенной линейной части должна иметь подъем для первой асимптоты на величину 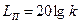для статических систем и такой же подъем при частоте 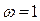для первой асимп­тоты в системах с линейной частью, обладающей астатизмом первого порядка. Нелинейность проявляет свои особенности только при формировании среднечастотной части желаемой л. а. х.

Если статические характеристики имеют зону нечувстви­тельности (рис. 7.16, б) при любом дальнейшем продолжении, то установившаяся ошибка в основном будет определяться половиной зоны нечувствительности. Переходный равновесно схо­дящийся процесс может закончиться при любом значении вход­ной величины нелинейности внутри зоны нечувствительности 2б. В этом случае коэффициент передачи нелинейного звена для определения подъема, желаемой л. а. х. рекомендуется опреде­лять методом статической линеаризации, т. е. взятием отноше­ния ординат в области, прилегающей к зоне нечувствительности, к абсциссам нелинейной статической характеристики (рис. 7.16,б). После получения общего коэффициента передачи 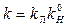подъем желаемой л. а. х. линейной части определяется по пра­вилам линейных систем.