Определение показателя колебательности в нелинейных системах

Пусть имеем нелинейную систему (рис. 7.1), состоящую из линейной части с передаточной функцией 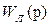и нелинейного звена со статической нелинейной характеристикой .

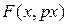Для линейной части, согласно ее передаточной функции, имеем частотную передаточную функцию

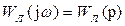(7.1)

при .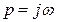

Рис. 7.1. Нелинейная система

Для нелинейного звена после выполнения гармонической в линеаризации получим эквивалентную передаточную функцию (комплексный коэффициент передачи)

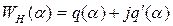(7.2)

Здесь амплитуда колебаний на входе нелинейности берется в относительных величинах ,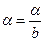

где b — характерное зна­чение x на статической характеристике нелинейного звена.

Эк­вивалентная передаточная функция с относительной амплиту­дой в качестве аргумента называется нормированной.

Частотная передаточная функция для гармонически линеа­ризованной замкнутой системы, согласно (7.1) и (7.2), будет

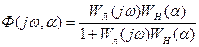
или

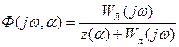(7.3)

где 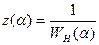— обратная эквивалентная передаточная функция нелинейного звена.

Входящие в (7.3) комплексные величины имеют значения:

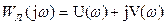
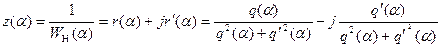(7.4)

По аналогии с линейными системами за показатель колеба­тельности для гармонически линеаризованной системы примем

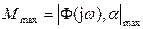
Геометрические места 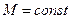для нелинейной системы на плоскости U, jV можно найти по выражению

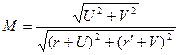(7.5)

так как теперь вместо единицы в частотной передаточной функ­ции линейной замкнутой системы

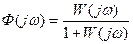
в нелинейной системе, согласно (7.3) и (7.4), имеем обратную эквивалентную передаточную функцию нелинейного звена

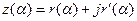
Проделав преобразования выражения (7.5) полу­чим уравнение

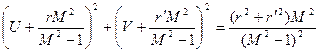
или 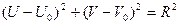(7.6)

где

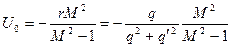
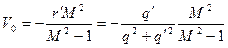(7.7)

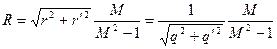
Из (7.6) и (7.7) следует, что при различных относительных амплитудах на входе нелинейного звена постоянному значению 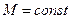в нелинейной системе соответствует множество ок­ружностей различных радиусов с центрами, смещенными как по оси вещественных, так и по оси мнимых. Запретные зоны для амплитудно-фазовой частотной характеристики линейной части системы 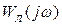теперь образуются касательными конту­рами, охватывающими эти окружности (рис. 7.2,а).

В случае однозначных нечетно-симметричных нелинейностей при 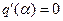, , 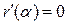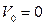уравнения окружностей принимают вид

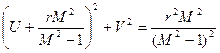
или ,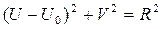

где 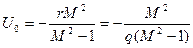(7.8)

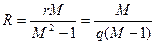(7.9)

Для определения показателя колебательности в нелинейной системе следует на комплексной плоскости U, jV построить запретные зоны 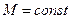и амплитудно-фазовую характери­стику линейной части 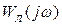. За значение показателя колеба­тельности принимается значение М той запретной зоны, кото­рой касается характеристика 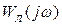не заходя в нее (рис. 7.2,а). Как видим, нелинейные свойства систем отражаются в расширении и смещении запретных зон 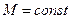по сравнению с линейными системами.

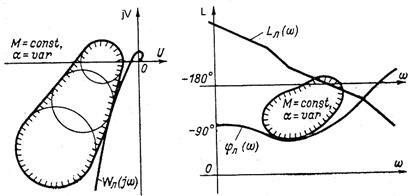
а) б)

Рис. 7.2. Запретные зоны для АФЧХ

линейной части системы

Деформации запретных зон происхо­дят за счет изменения коэффициентов гармонической линеариза­ци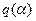и и 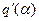при изменении относительной амплитуды 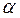, на входе нелинейного звена. Пр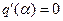и и 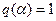имеем линейную систему с запретной зоной в виде одной окружности как частный случай нелинейных систем.

Запретные зоны для 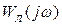с комплексной плоскости мо­гут быть перестроены в запретные зоны для фазовой характери­стики линейной части 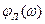на логарифмической плоскости (рис. 7.2, б), как это было показано для линейных систем.

а) б)

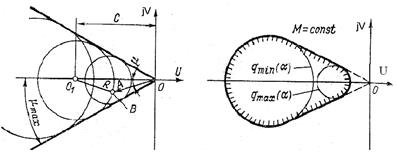
Рис. 7.3. Определение запаса по фазе

Для нелинейных систем с однозначными нечетно-симмет­ричными статическими нелинейностями построение запретных зон 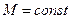на комплексной и логарифмической плоскостях весьма упрощается, так как максимальный запас по фазе μ_mах в этом случае не зависит от значения амплитуды 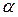. Действи­тельно, запас по фазе определяется по теореме косинусов из треугольника ОВ0₁ для любой из окружностей 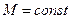, 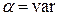(рис. 7.3, а) и при учете значений

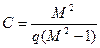
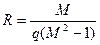
составит величину

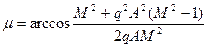(7.10)

максимальное значение запаса по фазе будет при R, перпен­дикулярном А:

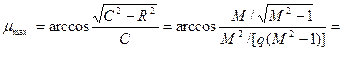
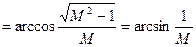(7.11)

Как видим, в полученное выражение для μ_mах не входит (величина 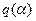и, следовательно, максимальное значение запаса по фазе для нелинейной системы с нечетно симметричной нели­нейностью определяется только показателем колебательности М совпадает с максимальным значением запаса по фазе линейной системы, полученной из нелинейной исключением нелинейности.

При построении запретных зон для амплитудно-фазовой характеристики линейной части системы на комплексной плоскости в этом случае достаточно построить окружности 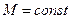, соответствующие 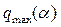и 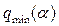, и соединить их касательными (рис. 7.3, б). Область ограничения указанными окружностями и касательными и будет запретной зоной 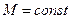для амплитудно-фазовой характеристики линейной части.

Для динамических нелинейностей, когда коэффициенты гармонической линеаризации зависят от амплитуды и частоты, эквивалентная передаточная функция нелинейного звена 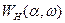изображается в виде семейства характеристик 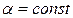или 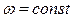. Запретные зоны для амплитудно-фазо­вой характеристики линейной части образуются в этом случае, как огибающие для всех областей, соответствующих отдельно взятым характеристикам.