Статистическое оценивание

Точечные оценки неизвестных параметров законов распределения

Здесь мы рассматриваем задачи определения неизвестных параметров законов распределения случайных величин в условиях относительно малых объемов эмпирических данных. Ясно, что каким бы не был объем выборки, значение параметра, который мы оцениваем, будет приближенным. Это приближение называется оценкой параметра. Для того чтобы оценка была наилучшей, требуется иметь о ней наиболее полное представление.

Пусть случайная величина x распределена по закону, который содержит неизвестный параметр 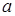. Требуется найти для него подходящую оценку 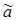по результатам выборки:

.

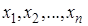При выборе условий, налагаемых на оценку 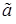неизвестного параметра 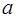прежде мы должны построить математическую модель эксперимента. Под этим мы понимаем следующее:

1) выборка является n–мерным случайным вектором

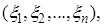
где случайные величины 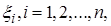определены на одном и том же пространстве элементарных событий и имеют, соответственно, одну и ту же функцию распределения и, тем самым, одни и те же параметры;

2) выборка репрезентативна, то есть любой элемент пространства элементарных событий имеет одинаковую вероятность попасть в выборку.

Таким образом, оценка 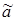параметра 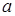есть n–мерная неслучайная функция n случайных аргументов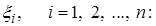

.

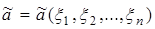Принято считать, что оценка 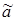должна удовлетворять условиям:

а) несмещенности:

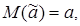
практически это означает, что систематические ошибки отсутствуют;

б) эффективности, то есть оценка 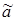более эффективна чем 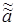, если

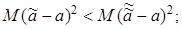
эффективность оценки 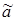означает, что её дисперсия меньше, чем дисперсия других оценок;

в) состоятельности, то есть

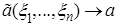при

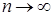
состоятельность означает, что для оценки 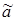выполняется закон больших чисел.

Для оценки математического ожидания 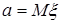случайной величины x всем условиям удовлетворяет средняя арифметическая :

.

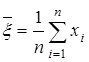Для оценки дисперсии, в условиях выборок относительно большого объема, используется выборочная дисперсия:

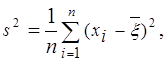
или

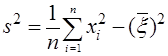
Выборочная дисперсия не удовлетворяет условию несмещенности.

Всем трем условиям удовлетворяет исправленная дисперсия:

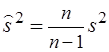
или

.

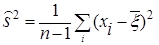Рассмотренные выше оценки называются точечными.