Интервальное оценивание
Рассмотренные оценки 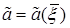 , как правило, не совпадают с истинным значением параметра a. Следовательно, имеет место некоторая погрешность при замене параметра его оценкой, то есть,
, как правило, не совпадают с истинным значением параметра a. Следовательно, имеет место некоторая погрешность при замене параметра его оценкой, то есть, 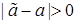 , хотя величина этой погрешности неизвестна. Чтобы получить представление о точности и надежности оценки
, хотя величина этой погрешности неизвестна. Чтобы получить представление о точности и надежности оценки 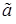 неизвестного параметра a в математической статистике рассматривают оценку
неизвестного параметра a в математической статистике рассматривают оценку
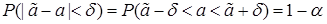 .
.
Вероятность того, что случайный интервал 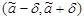 накроет неизвестный параметр a, равна
накроет неизвестный параметр a, равна 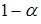 и называется доверительной вероятностью. Причем, чем меньше будет
и называется доверительной вероятностью. Причем, чем меньше будет 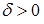 для заданной вероятности
для заданной вероятности 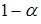 , тем точнее оценка
, тем точнее оценка 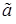 . Заметим, что если
. Заметим, что если 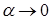 , то
, то 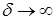 .
.
Случайный интервал, определяемый результатами наблюдений, который с заданной вероятностью 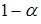 накрывает неизвестный параметр a, называется доверительным интервалом для параметра a, соответствующим доверительной вероятности
накрывает неизвестный параметр a, называется доверительным интервалом для параметра a, соответствующим доверительной вероятности 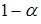 .
.
Пусть задана выборка 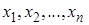 значений случайной величины x, распределенной по нормальному закону с плотностью
значений случайной величины x, распределенной по нормальному закону с плотностью 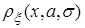 , содержащей два неизвестных параметра a и s. По заданной выборке доверительный интервал параметра
, содержащей два неизвестных параметра a и s. По заданной выборке доверительный интервал параметра 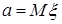 получается на основе распределения Стьюдента.
получается на основе распределения Стьюдента.
Теорема. Если 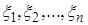 - независимые случайные величины распределенные нормально с математическими ожиданиями a и дисперсиями
- независимые случайные величины распределенные нормально с математическими ожиданиями a и дисперсиями 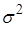 , то случайная величина
, то случайная величина 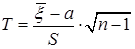 имеет распределение Стьюдента с
имеет распределение Стьюдента с 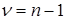 числом степеней свободы.
числом степеней свободы.
Доверительный интервал для математического ожидания случайной величины распределенной по нормальному закону имеет вид:
1) если s - неизвестно, то
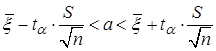 ,
, 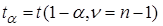 ;
;
2) если s - известно, то
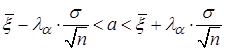 .
.
Зная число степеней свободы 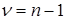 и доверительную вероятность a параметр (квантиль)
и доверительную вероятность a параметр (квантиль) 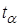 находится по таблице, параметр (квантиль)
находится по таблице, параметр (квантиль) 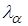 находится из уравнения
находится из уравнения 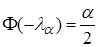 , где
, где 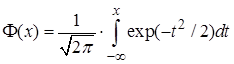 .
.
Для построения доверительного интервала для дисперсии используют распределение 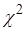 .
.
Пусть 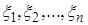 - независимые случайные величины распределенные нормально с
- независимые случайные величины распределенные нормально с 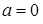 ,
, 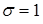 . Случайная величина
. Случайная величина 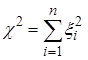 называется случайной величиной с распределением
называется случайной величиной с распределением 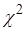 с
с 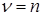 степенями свободы.
степенями свободы.
Доверительный интервал для дисперсии случайной величины распределенной по нормальному закону имеет вид:
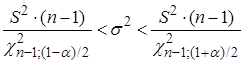 .
.
Значения функции 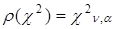 приводятся в таблице.
приводятся в таблице.
Пример.Найти доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания нормально распределенной случайной величины, представленной выборкой объема 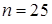 , для которой найдены выборочное среднее
, для которой найдены выборочное среднее 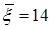 , если известно, что среднее квадратичное отклонение
, если известно, что среднее квадратичное отклонение 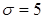 .
.
◄ Поскольку для нормально распределенной случайной величины известно среднее квадратичное отклонение, то воспользуемся формулой
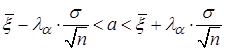 ,
,
где параметр (квантиль) 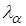 найдем из равенства
найдем из равенства 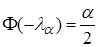 , при условии
, при условии 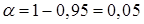 , получаем
, получаем
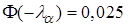 , т.е.
, т.е. 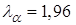 .
.
Составим доверительный интервал
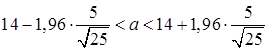 ,
,
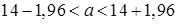 ,
,
окончательно получаем
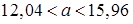 .►
.►
Дата добавления: 2016-07-27; просмотров: 2103;











