Интервальное оценивание
Мы уже знаем, что 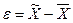 . Если
. Если 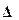 представляет собой предел, которым ограничена сверху абсолютная величина
представляет собой предел, которым ограничена сверху абсолютная величина 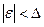 , то
, то 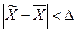 . Следовательно,
. Следовательно,
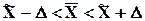 (7.4)
(7.4)
Мы получили интервальную оценку генеральной средней. Из теоремы Чебышева следует, что
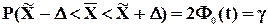 . (7.5)
. (7.5)
Интервальной оценкой называют оценку, которая определяется двумя числами - концами интервала, который с определенной вероятностью накрывает неизвестный параметр генеральной совокупности. Интервал, содержащий оцениваемый параметр генеральной совокупности, называют доверительным интервалом.Для его определения вычисляется предельная ошибка выборки 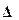 , позволяющая установить предельные границы, в которых с заданной вероятностью (надёжностью) должен находиться параметр генеральной совокупности.
, позволяющая установить предельные границы, в которых с заданной вероятностью (надёжностью) должен находиться параметр генеральной совокупности.
Предельная ошибка выборки равна t-кратному числу средних ошибок выборки. Коэффициент t позволяет установить, насколько надежно высказывание о том, что заданный интервал содержит параметр генеральной совокупности. Если мы выберем коэффициент таким, что высказывание в 95% случаев окажется правильным и только в 5% - неправильным, то мы говорим: со статистической надежностью в 95% доверительный интервал выборочной статистики содержит параметр генеральной совокупности.Статистической надежности в 95% соответствует доверительная вероятность - 0,95. В 5% случаев утверждение "параметр принадлежит доверительному интервалу" будет неверным. То есть 5% задает уровень значимости ( 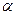 ) или 0,05 вероятность ошибки. Обычно в статистике уровень значимости выбирают таким, чтобы он не превысил 5% (
) или 0,05 вероятность ошибки. Обычно в статистике уровень значимости выбирают таким, чтобы он не превысил 5% ( 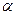 < 0,05). Доверительная вероятность и уровень значимости дополняют друг друга до 1 (или 100%) и определяют надежность статистического высказывания.
< 0,05). Доверительная вероятность и уровень значимости дополняют друг друга до 1 (или 100%) и определяют надежность статистического высказывания.
С помощью доверительного интервала можно оценить не только генеральную среднюю, но и другие неизвестные параметры генеральной совокупности.
Для оценкиматематического ожидания а (генеральной средней)[5]нормально распределенного количественного признака Х по выборочной средней 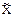 при известном среднем квадратическом отклонении sгенеральной совокупности (на практике - при большом объеме выборки, т.е. при n ³ 30) и собственно-случайном повторном отборе формула (7.5.2) примет вид:
при известном среднем квадратическом отклонении sгенеральной совокупности (на практике - при большом объеме выборки, т.е. при n ³ 30) и собственно-случайном повторном отборе формула (7.5.2) примет вид:
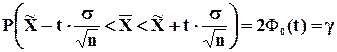 (7.6)
(7.6)
где t определяется по таблицам функции Лапласа из соотношения
2F0(t) = g;
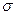 - среднее квадратическое отклонение;
- среднее квадратическое отклонение;
n - объем выборки (число обследованных единиц).
D определяется по формуле:
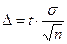
Для оценки математического ожидания а (генеральной средней) нормально распределенного количественного признака Х по выборочной средней 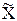 при известном среднем квадратическом отклонении sгенеральной совокупности (при большом объеме выборки, т.е. при n
при известном среднем квадратическом отклонении sгенеральной совокупности (при большом объеме выборки, т.е. при n 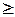 30) и собственно-случайном бесповторном отборе формула (7.6) примет вид:
30) и собственно-случайном бесповторном отборе формула (7.6) примет вид:
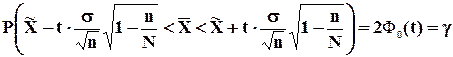 (7.7)
(7.7)
D определяется по формуле:

Для оценки математического ожидания а (генеральной средней) нормально распределенного количественного признака Х по выборочной средней 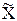 при неизвестном среднем квадратическом отклонении s генеральной совокупности (на практике - при малом объеме выборки, т.е. при n < 30) и собственно-случайном повторном отборе формула (7.6) примет вид:
при неизвестном среднем квадратическом отклонении s генеральной совокупности (на практике - при малом объеме выборки, т.е. при n < 30) и собственно-случайном повторном отборе формула (7.6) примет вид:
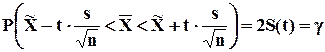 (7.8)
(7.8)
где t определяется по таблицам Стьюдента
по уровню значимости a = 1 - g
и числу степеней свободы k = n - 1;
s - исправленное выборочное среднее квадратическое отклонение;
n - объем выборки.
D определяется по формуле:
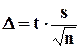
Для оценки математического ожидания а (генеральной средней) нормально распределенного количественного признака Х по выборочной средней 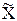 при неизвестном среднем квадратическом отклонении s генеральной совокупности (при малом объеме выборки, т.е. при n < 30) и собственно-случайном бесповторном отборе формула (7.8) примет вид:
при неизвестном среднем квадратическом отклонении s генеральной совокупности (при малом объеме выборки, т.е. при n < 30) и собственно-случайном бесповторном отборе формула (7.8) примет вид:
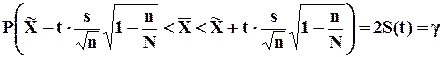 (7.9)
(7.9)
D определяется по формуле:
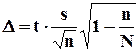
Для оценки генеральной доли р нормально распределенного количественного признака по выборочной доле 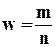 при большом объеме выборки, т.е. при n
при большом объеме выборки, т.е. при n 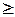 30) и собственно-случайном повторном отборе формула (7.5) примет вид:
30) и собственно-случайном повторном отборе формула (7.5) примет вид:
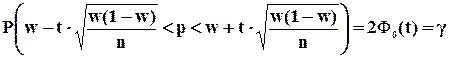 (7.10)
(7.10)
где t определяется по таблицам функции Лапласа из соотношения
2F0(t) = g;
w - выборочная доля;
n - объем выборки (число обследованных единиц).
D определяется по формуле:
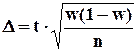
Для оценки генеральной доли р нормально распределенного количественного признака по выборочной доле 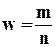 при большом объеме выборки, т.е. при n
при большом объеме выборки, т.е. при n 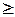 30 и собственно-случайном бесповторном отборе формула (7.10) примет вид:
30 и собственно-случайном бесповторном отборе формула (7.10) примет вид:
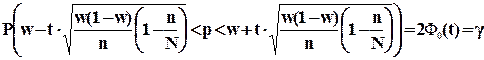 (7.11)
(7.11)
D определяется по формуле:
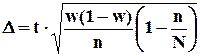
Для оценки генеральной доли р нормально распределенного количественного признака по выборочной доле 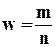 при малом объеме выборки, т.е. при n < 30 и собственно-случайном повторном отборе формула (7.10) примет вид:
при малом объеме выборки, т.е. при n < 30 и собственно-случайном повторном отборе формула (7.10) примет вид:
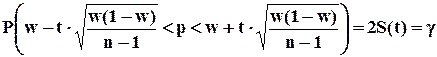 (7.12)
(7.12)
где t определяется по таблицам Стьюдента
по уровню значимости a = 1 - g
и числу степеней свободы k = n - 1.
D определяется по формуле:
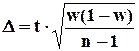
Для оценки генеральной доли р нормально распределенного количественного признака по выборочной доле 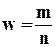 при малом объеме выборки, т.е. при n < 30 и собственно-случайном бесповторном отборе формула (7.12) примет вид:
при малом объеме выборки, т.е. при n < 30 и собственно-случайном бесповторном отборе формула (7.12) примет вид:
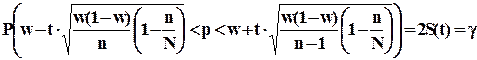 (7.13)
(7.13)
D определяется по формуле:
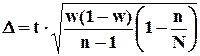
Дата добавления: 2016-10-26; просмотров: 2478;











