Микрочастицы и макроскопические системы . Термодинамическое и статистическое описание идеального электронного газа.

Статистика носителей зарядов в полупроводниках и металлах

Основные понятия статистической физики.

Статистическая физика это раздел теоретической физики в котором изучается макроскопические свойства системы состоящей из очень большого количества частиц на основании молекулярно- кинетических представлений и методов математической статистики основанных на теории вероятностей.
Под вероятностью понимается предел, к которому стремится относительная частота появления некоторого события при достаточно большом, стремящемся к бесконечности числе повторений опыта при неизменных внешних условиях.
Если при N опытах n раз получено определенное событие, то вероятность этого события

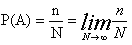
Величина P испытывает лишь небольшие колебания около некоторого числового значения при любых, достаточно больших значениях числа опытов N.
Если Р(А)=1, то событие А достоверное.
Если Р(А)=0, то событие А невозможное.

Функция f(x,y,z) называется функцией распределения или плотностью вероятности.

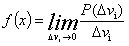
или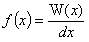
Плотность вероятности представляет собой вероятность того что некоторая случайная величина Х примет значение в единичном интервале около некоторого фиксированного значения x0

Микрочастицы и макроскопические системы . Термодинамическое и статистическое описание идеального электронного газа.

Для решения задач физики твердого тела (электронный газ в металлах), физики конденсированного состояния (сверхтекучесть), астрофизики (свойства белых карликов и нейтронных звезд) широко применяется модель квантового газа

Квантовый газ — газ, состоящий из (квази)частиц, де-бройлевская длина волны которых намного превышает их радиус взаимодействия.

Свойства квантового газа зависят от степени его вырождения, характеризующегося температурой вырождения. Температура вырождения T₀ зависит от плотности газа, 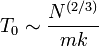, N — концентрация частиц, m — масса частицы, k — постоянная Больцмана. При условии 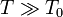газ является невырожденным и распределение частиц по энергиям описывается распределением Больцмана. В случае 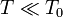газ попадает в область квантового вырождения и представляет собой, в зависимости от статистики частиц, вырожденный Ферми-газ (полуцелый спин, Статистика Ферми — Дирака) или Бозе-газ (целый спин, Статистика Бозе — Эйнштейна).

Различают идеальный (пренебрежение взаимодействием частиц) и реальный квантовый газ

Электроны, как частицы электронного газа , обладающие полуцелым спином, подчиняются статистике Ферми – Дирака. Вероятность того, что электрон будет находиться в квантовом состоянии с энергией Е, выражается функцией Ферми – Дирака:

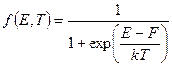. (4.1)

Здесь F – электрохимический потенциал, или уровень Ферми. Из (4.1) видно, что уровень Ферми можно определить как энергию такого квантового состояния, вероятность заполнения которого равна ½.

Вид функции Ферми – Дирака схематически показан на рисунке 1.4.

При Т = 0 она имеет вид разрывной функции.

Для E < F она равна 1, а значит, все квантовые состояния при E < F заполнены электронами.

Для E > F функция f = 0 и соответствующие квантовые состояния совершенно не заполнены.

При Т > 0 функция Ферми изображается непрерывной кривой и в узкой области энергий, порядка нескольких kT, в окрестности точки E = F быстро изменяется от 1 до 0. Размытие функции Ферми тем больше, чем выше температура.

Вычисление различных статистических величин значительно упрощается, если уровень Ферми F лежит в запрещенной зоне энергий и удален от края зоны Е_C хотя бы на 2kT (в некоторых учебниках пишут Е_C – Е > kT). Тогда в распределении (1.7) единицей в знаменателе можно пренебречь и оно переходит в распределение Максвелла – Больцмана классической статистики. Это случай невырожденного полупроводника:

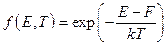. (4.2)

Концентрация электронов в зоне проводимости равна:

.

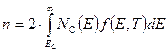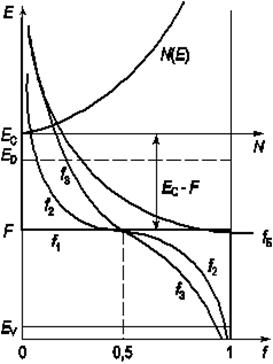
Рис. 4.1. Функция распределения плотности состояний в зоне проводимости N(E), функции Ферми – Дирака f и Больцмана f_Б

Подставляем в (4.2) выражения (3.4) и (4.1). Получим:

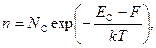(4.4) (4.3)

где

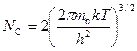. (4.4)

Величина N_C получила название эффективной плотности состояний в зоне проводимости.

В случае невырожденного полупроводника, когда уровень Ферми лежит выше потолка валентной зоны хотя бы на 2kT, то есть F – E_C > 2kT (в некоторых учебниках пишут F – E_C > kT), функция Ферми – Дирака для дырок f_p имеет вид:

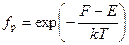, (4.5)

а концентрация дырок в валентной зоне

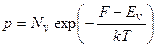, (4.6)

где E_V – энергия, соответствующая потолку валентной зоны, а N_V рассчитывается по уравнению (1.11), если вместо m_n взять эффективную массу дырки m_p. Величина N_V – эффективная плотность состояний в валентной зоне.