Распределение некоторых случайных величин, представляющих функции нормальных величин
Наиболее важную роль в математической статистике играет распределение Пирсона, иначе называемое 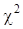 - распределением. Этому распределению подчинена сумма квадратов k независимых случайных величин:
- распределением. Этому распределению подчинена сумма квадратов k независимых случайных величин:
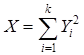 , ,
| (13) |
каждая из которых, в свою очередь, распределена по стандартному нормальному закону. Плотность 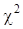 -распределения
-распределения
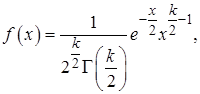
| (14) |
где 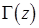 – гамма-функция:
– гамма-функция:
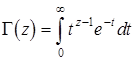 . .
|
Графики плотности 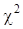 - распределения приведены на рис.:
- распределения приведены на рис.:
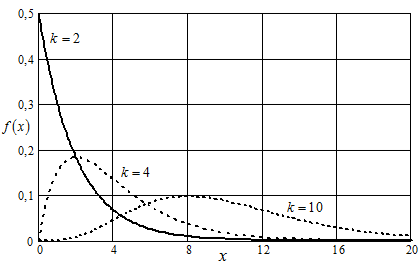
Рис. Плотность 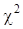 - распределения для различного числа степеней свободы
- распределения для различного числа степеней свободы
С увеличением числа степеней свободы плотность (14) приближается к плотности нормального закона. Справедлива асимптотическая формула
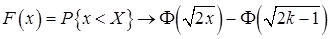 , ,
|
где 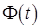 – функция стандартного нормального распределения.
– функция стандартного нормального распределения.
Распределением Стьюдента с k степенями свободы называется распределение случайной величины:
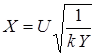 , ,
| (15) |
где U – случайная величина, подчиненная стандартному нормальному закону, Y – случайная величина, подчиненная 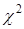 ‑ распределению с k степенями свободы.
‑ распределению с k степенями свободы.
Плотность распределения Стьюдента
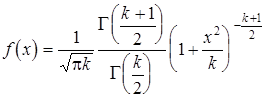 . .
| (16) |
Графики функции (16) для различного числа степеней свободы 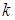 изображены на рис.:
изображены на рис.:
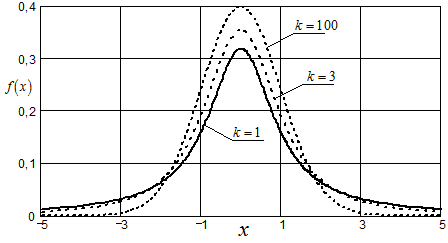
Рис. Плотность распределения Стьюдента
Распределением Фишера, или F-распределением с m и n степенями свободы называется распределение случайной величины
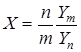 , ,
| (17) |
где 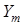 ,
, 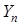 – случайные величины, подчиненные
– случайные величины, подчиненные 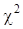 ‑ распределениям со степенями свободы m и n, соответственно.
‑ распределениям со степенями свободы m и n, соответственно.
Плотность F-распределения:
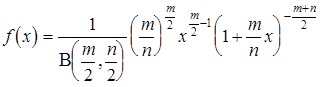 , ,
| (18) |
где
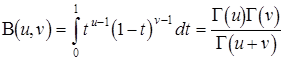 – бета-функция. – бета-функция.
|
Графики (18) изображены на рис.:
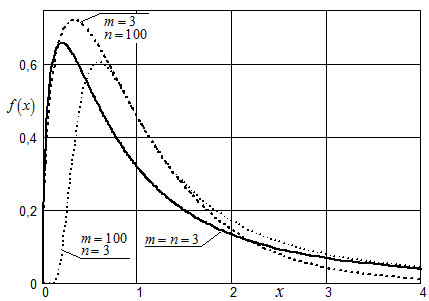
Рис. Плотность F-распределения
Дата добавления: 2016-07-27; просмотров: 2771;











