Выборка и способы ее записи. Графическое представление выборки
Математическая статистика – раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для теоретических исследований и практических выводов.
Статистические данные – набор числовых значений, представленных в виде выборки из генеральной совокупности Г, являющейся отображением реального явления в числовое множество.
Математическая статистика не раздел теории вероятностей, а самостоятельная наука со своими понятиями, методами и способами исследования. Изучает как случайные, так и детерминированные явления на основе более или менее обширного статистического материала.
Образно говоря, теория вероятностей, зная все о генеральной совокупности, изучает состав ее выборок. Математическая статистика решает обратную задачу: по изучению состава отдельных выборок пытается получить как можно больше информации о генеральной совокупности.
Основными понятиями математической статистики являются «генеральная совокупность», «выборка», «эмпирическая функция распределения» и «параметры распределения».
Рассмотрим случайный эксперимент, который описывается одномерной случайной величиной x. Множество всех возможных значений случайной величины x будем называть генеральной совокупностью G. Осуществив n независимых повторений эксперимента, получим совокупность n значений случайной величины x, которые обозначим 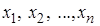 . Заметим, что среди этих чисел могут быть и равные.
. Заметим, что среди этих чисел могут быть и равные.
Совокупность 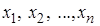 ,
, 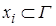 ,
, 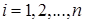 ,
, 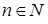 , называется выборкой, а число элементов, входящих в выборку, - ее объемом.
, называется выборкой, а число элементов, входящих в выборку, - ее объемом.
Если провести другую серию из n независимых повторений этого же эксперимента, то получится, вообще говоря, уже другая выборка значений случайной величины x. Поэтому в теоретических исследованиях выборка n значений случайной величины x представляется случайным вектором 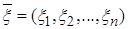 , где
, где 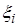 ,
, 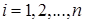 , - независимые случайные величины, заданные на одном и том же вероятностном пространстве и имеющие одну и ту же функцию распределения
, - независимые случайные величины, заданные на одном и том же вероятностном пространстве и имеющие одну и ту же функцию распределения 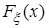 , причем
, причем 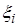 - одно из возможных, заранее неизвестных, значений случайной величины x в i-ом повторении эксперимента.
- одно из возможных, заранее неизвестных, значений случайной величины x в i-ом повторении эксперимента.
Задачей исследования в математической статистике является построение математической модели случайного эксперимента, проверка адекватности модели изучаемому явлению и, в случае положительного ответа, прогнозирование появления события, как части явления. При построении математической модели предполагается, что выборка репрезентативна, то есть, любой элемент генеральной совокупности имеет одинаковую вероятность попасть в выборку.
К основным задачам математической статистики относятся: 1) оценка функции распределения; 2) оценка неизвестных параметров; 3) проверка априорных предположений или статистических гипотез.
Пусть задана выборка
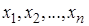 .
.
Элементы выборки, представленные в порядке неубывания элементов, 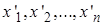 , причем
, причем 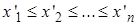 , образуют вариационный ряд.
, образуют вариационный ряд.
Размахом выборки 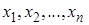 называется величина равная разности наибольшего и наименьшего элементов выборки, то есть,
называется величина равная разности наибольшего и наименьшего элементов выборки, то есть,
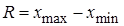 ,
,
где 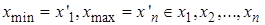 .
.
Пусть в выборке 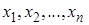 k различных элементов
k различных элементов 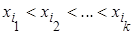 . Числа
. Числа 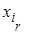 ,
, 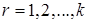 , называются вариантами или наблюдениями. Число появлений варианты
, называются вариантами или наблюдениями. Число появлений варианты 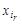 называется абсолютной частотой
называется абсолютной частотой 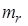 ,
, 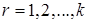 .
.
Варианты и соответствующие им абсолютные частоты можно представить в виде таблицы, называемой статистическим рядом распределения (простой статистической таблицей) абсолютных частот:
| x | 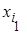
| 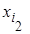
| … | 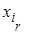
|
| m | 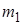
| 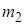
| … | 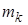
|
Если на плоскости построить точки ( 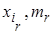 ),
), 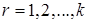 , и соединить их отрезками прямых, то полученная ломанная называется полигоном абсолютных частот:
, и соединить их отрезками прямых, то полученная ломанная называется полигоном абсолютных частот:
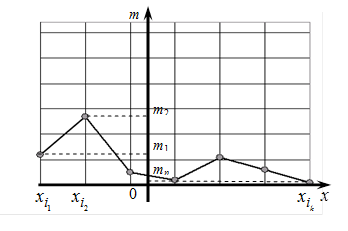
Если x - непрерывная случайная величина, то весь диапазон ее значений делят на k интервалов (длины которых определяют по формуле 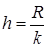 ,
, 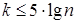 ) и подсчитывают количество
) и подсчитывают количество 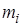 ,
, 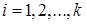 , вариант, попавших в данный интервал. По абсолютным частотам каждого из интервалов находят относительные частоты
, вариант, попавших в данный интервал. По абсолютным частотам каждого из интервалов находят относительные частоты 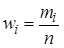 ,
, 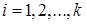 . Очевидно,
. Очевидно, 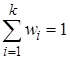 .
.
Полученные интервалы и соответствующие относительные частоты 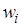 записывают в виде таблицы, называемой интервальным статистическим рядом распределения (интервальной статистической таблицей):
записывают в виде таблицы, называемой интервальным статистическим рядом распределения (интервальной статистической таблицей):
| x | 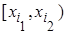
| 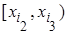
| … | 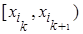
|
| w | 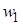
| 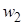
| … | 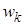
|
Графическим представлением интервального статистического ряда является гистограмма:
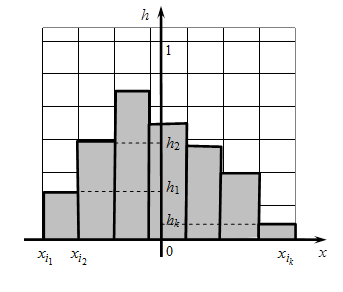
Для ее построения по оси абсцисс откладывают интервалы и на каждом из них строят прямоугольники высотой 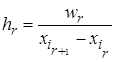 ,
, 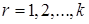 .
.
Площадь гистограммы равна 1. В теории вероятностей гистограмме соответствует график плотности распределения вероятностей.
Замечание. На основании гистограммы можно построить полигон частот. Для этого достаточно соединить середины верхних сторон прямоугольников отрезками прямых. В этом случае непрерывную случайную величину можно рассматривать как дискретную, эмпирические значения которой совпадают с координатами 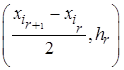 ,
, 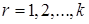 .
.
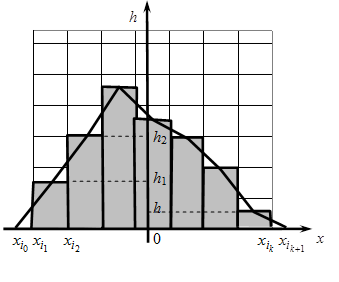
Гистограмму и полигон частот используют для подбора модели распределения изучаемой случайной величины x.
Эмпирической функцией распределения 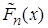 называется относительная частота события (
называется относительная частота события ( 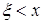 ) в данной выборке значений случайной величины x, то есть,
) в данной выборке значений случайной величины x, то есть, 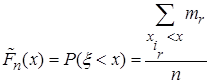 , где
, где 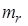 - число
- число 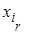 меньших x,
меньших x, 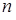 - объем выборки.
- объем выборки.
В силу закона больших чисел эмпирическая функция распределения 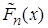 является оценкой подлинной функции распределения
является оценкой подлинной функции распределения 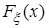 при
при 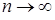 , поэтому функция
, поэтому функция 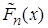 обладает свойствами в полнее аналогичными
обладает свойствами в полнее аналогичными 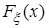 :
:
1) 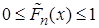 ,
, 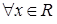 ;
;
2) функция 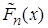 является неубывающей функцией;
является неубывающей функцией;
3) если 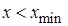 , то
, то 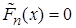 , если
, если 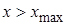 , то
, то 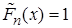 .
.
Функция 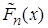 - ступенчатая, возрастает скачками, которые соответствуют наблюдениям, и равны относительным частотам этих значений:
- ступенчатая, возрастает скачками, которые соответствуют наблюдениям, и равны относительным частотам этих значений:
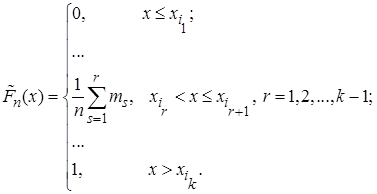
Дата добавления: 2016-07-27; просмотров: 6918;











