Числовые оценки параметров распределения
В качестве характеристик выборки значений случайной величины x в статистике рассматриваются различные средние (средняя гармоническая, средняя арифметическая, средняя квадратическая и др.), а также мода и медиана.
Модой 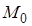 выборки значений случайной величины x называется та варианта, которая наиболее часто встречается в выборке.
выборки значений случайной величины x называется та варианта, которая наиболее часто встречается в выборке.
Медианой 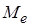 выборки значений случайной величины x называется варианта, расположенная в середине вариационного ряда этой выборки. Если выборка состоит из четного числа членов, то медиана рассчитывается как средняя арифметическая серединных элементов вариационного ряда.
выборки значений случайной величины x называется варианта, расположенная в середине вариационного ряда этой выборки. Если выборка состоит из четного числа членов, то медиана рассчитывается как средняя арифметическая серединных элементов вариационного ряда.
Наилучшей оценкой математического ожидания случайной величины x является выборочная средняя (средняя арифметическая взвешенная):
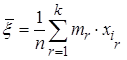 ,
,
а дисперсии – выборочная (статистическая) дисперсия:
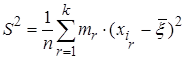 ,
,
при малых n – исправленная дисперсия:
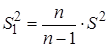 .
.
Оценка стандартного (среднего квадратичного) отклонения связана с оценкой дисперсии соотношением:
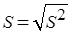 . .
|
Если выборочная средняя, мода и медиана совпадают, то выборка симметрична.
Пример.Для выборки: 6, 7, 6, 4, 6, 5, 7, 8, 6, 4, 2, 5, 2, 5, 4, 6, 6, 3, 5, 7
а) определить вариационный ряд и размах выборки;
б) построить простую статистическую таблицу и полигон частот;
в) построить интервальную таблицу и гистограмму;
г) найти эмпирическую функцию распределения и построить ее график;
д) найти выборочную среднюю, выборочную и исправленную дисперсию, моду, медиану.
◄ Упорядочивая выборку значений случайной величины получаем вариационный ряд:
2, 2, 3, 4, 4, 4, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6, 7, 7, 7, 8;
и находим размах выборки
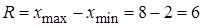 .
.
От вариационного ряда переходим к простой статистической таблице:
| x |
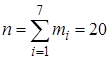
| |||||||
| m |
Построим полигон частот:

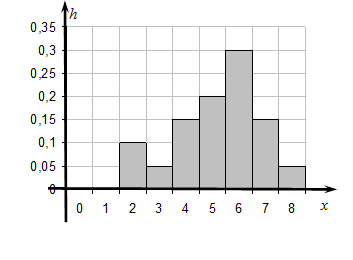
Построим интервальную статистическую таблицу и по ней гистограмму:
| x | 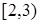
| 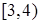
| 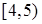
| 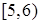
| 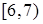
| 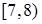
| 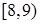
| |
| w | 0,10 | 0,05 | 0,15 | 0,20 | 0,30 | 0,15 | 0,05 | 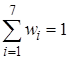
|
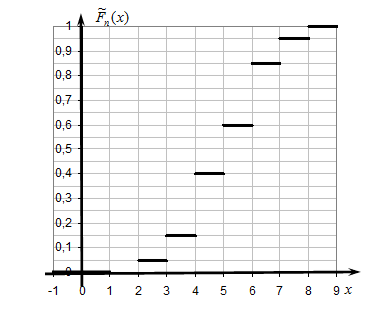
Найдем эмпирическую функцию распределения и построим ее график:
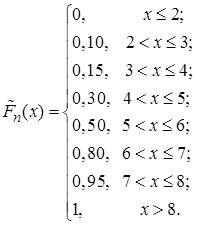
Вычислим выборочную среднюю
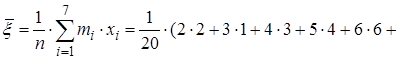
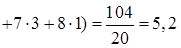 ,
,
выборочную и исправленную дисперсию
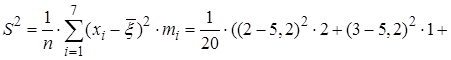
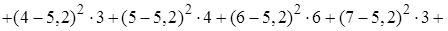
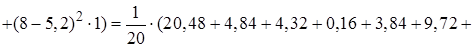
 ,
,
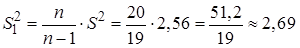 .
.
Находим выборочные моду и медиану:
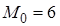 ,
,
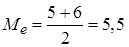 .►
.►
Дата добавления: 2016-07-27; просмотров: 4089;











