НЕПОЛНОЕ СТАТИСТИЧЕСКОЕ ОПИСАНИЕ ДАННЫХ НАБЛЮДЕНИЯ. ПАРАМЕТРИЧЕСКОЕ ОПИСАНИЕ АПРИОРНОЙ НЕОПРЕДЕЛЕННОСТИ

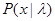Сказанное выше о статистическом описании параметров , можно отнести и к данным наблюдения х. В соответствии с фактическим объе­мом знаний функция правдоподобия может быть определена с той степенью подробности, которая характерна для случаев, перечис­ленных в § 3.1. При этом аналогично классу 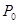можно ввести класс 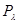распределений вероятности (функций правдоподобия) для наблюдаемых данных х, к которому принадлежат все возможные при данном состоянии наших знаний распределения вероятности х ( 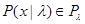). Этот класс, естественно, зависит от параметров функции правдоподобия , определяющих последствия принимаемых решений и соответствующие им потери.

Однако, пожалуй, наиболее универсальным способом статистиче­ского описания априорной неопределенности и учета имеющихся ограниченных сведений применительно как к данным наблюдения х, так и к ненаблюдаемым параметрам , является параметрический способ, который рассмотрим более подробно.

Пусть, например, совокупность данных наблюдения х представляет собой последовательность 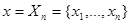, о которой известно, что все ее компоненты - независимые нормально распределенные величины с математическими ожиданиями 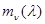, зависящими от , и неизвестной одинаковой дисперсией 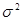. Это дает основание определить условную плотность вероятности – функцию правдоподобия 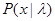с точностью до одного неизвестного параметра 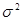, характеризующего интенсивность помехи, которая затрудняет наблюдение 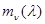и принятие решения относительно :

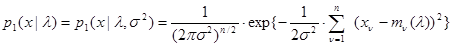. (3.2.1)

Приведенный пример - простейшая иллюстрация той распространенной на практике ситуации, когда имеющиеся априорные сведения качествен­ного характера (независимость и нормальность 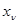) дают возможность задать структуру необходимых распределений вероятности с точностью до каких-либо дополнительных неизвестных параметров.

Немного усложним этот пример, предположив для конкретности, что может принимать всего два значения 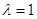и 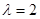(это соответст­вует задаче принятия двухальтернативного решения). Пусть при 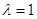математическое ожидание 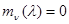при всех 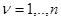и при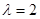

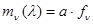, (3.2.2)

где 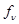- известные величины; а - неизвестный коэффициент. Этот услож­ненный случай соответствует, например, задаче обнаружения сигнала известной формы, но неизвестной интенсивности на фоне шума неизве­стной интенсивности. Как и в предыдущем примере, можно определить функцию правдоподобия 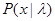с точностью до некоторого числа не­известных параметров, а именно

,

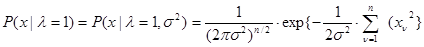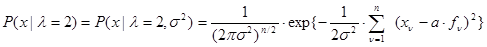, (3.2.3)

причем при 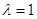функция правдоподобия зависит от одного неизвестно­го параметра 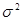, а при 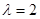- от совокупности двух параметров { 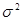, а} и для любых значений этих параметров полностью определена.

Если в общем случае обозначить через 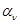совокупность дополни­тельных (по отношению к ) параметров, от которых зависит функция правдоподобия при данном значении , то подходящим выбором этих параметров можно добиться описания структуры функции правдопо­добия 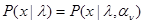, соответствующего имеющимся ограниченным статистическим сведениям относительно данных наблюдения х. В зави­симости от полноты и детальности этих сведений структура функции правдоподобия 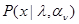может быть более или менее сложной, а ко­личество неизвестных параметров 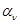велико или мало, но само пара­метрическое описание априорной неопределенности является практиче­ски универсальным способом учета ограниченных априорных сведений. По-видимому, стоит подчеркнуть, что в соответствии с введенным в гл. 2 определением как совокупности параметров, непосредственно влияю­щих на последствия от принятия решения и входящих в функцию по­терь, под 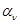понимаются все другие параметры, от которых зависит распределение вероятности данных наблюдения х. При этом возможны случаи, когда все или часть параметров 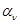физически однородны с па­раметрами .

Приведем еще примеры параметрического описания для априорных распределений вероятности 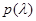.Рассмотрим сначала заведомо пре­дельный случай. Пусть , дискретно и имеет значения l = i = 1, …, m, которые могут приниматься с вероятностями 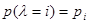. Если априор­ное распределение вероятности неизвестно, то в качестве неизвестных параметров могут рассматриваться сами эти вероятности 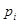, формальное задание которых с учетом естественных ограничений 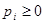, 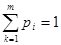определяет необходимое распределение вероятности через т - 1 неиз­вестный параметр.

Пусть далее представляет собой последовательность 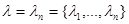, описывающую процесс, подлежащий фильтрации, или состояние управляемого объекта и т. п., и пусть известно, что эта по­следовательность удовлетворяет рекуррентному соотношению (при не­прерывном времени соответствующему дифференциальному равне­нию)

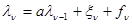, (3.2.4)

где 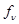- известные величины, возможно, зависящие от управляющего воздействия; а - неизвестный коэффициент; 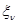- последовательности неза­висимых нормально распределенных величин с нулевым математическим ожиданием и одинаковой неизвестной дисперсией 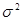. (Для случая, когда каждая из компонент 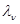и соответственно 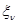являются векторами некото­рого порядка 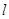, а - соответствующей матрицей порядк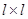а , а 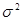заме­няется на неизвестную корреляционную матрицу порядка 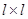, уравне­ние (3.2.4) описывает очень широкий класс линейных динамических объектов (или процессов) 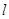-го порядка, испытывающих воздействие слу­чайных возмущений.) При этом соотношение (3.2.4) определяет марков­скую последовательность с переходной плотностью вероятности

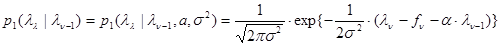, (3.2.5)

зависящей от двух неизвестных параметров а и 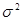. Полная плотность распределения вероятности 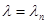определяется с помощью (3.2.5) по формуле (3.1.7) и также является функцией этих неизвестных параметров.

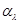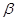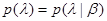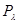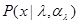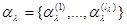По аналогии с обозначим через совокупность неизвестных па­раметров, от которых зависит априорное распределение вероятности с плотностью для параметров . В общем случае это дает возможность при ограниченных априорных сведениях о х и , задать - класс всех распределений известного вида , зависящих поми­мо , от совокупности неизвестных параметров и 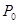- класс распределений вида 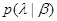, зависящих от совокупности неизвест­ных параметров 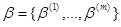. Разным значениям , вообще говоря, могут соответствовать различные наборы параметров 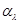со своей об­ластью изменения 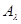( 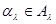). Очевидно, что подобно параметрам па­раметры 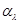являются аргументами функции правдоподобия 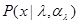. Отличие между этими двумя совокупностями заключается в том, что первая непосредственно влияет на последствия принимаемого решения и определяет величину потерь, в то время как совокупность параметров 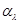не является аргументом функции потерь и не влияет на последствия решений непосредственно. Эта совокупность характеризует ту дополни­тельную неопределенность, которая имеет место из-за неполного знания статистических свойств наблюдаемых данных х при каждом данном зна­чении .

Совокупность параметров 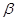используется для описания не полно­стью известной априорной статистики . Содержание этой совокупно­сти должно быть таково, чтобы имелась возможность определить с точностью до этих параметров априорное распределение вероятности с плотностью 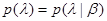при некоторых значениях 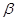из области зна­чений ( ).

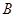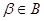Стоит отметить, что среди параметров 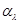и 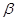могут быть одинако­вые, или даже совокупность параметров 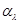может содержать в себе всю совокупность параметров 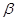. Пусть, например, исходное статистиче­ское описание данных наблюдения х состоит в задании плотности рас­пределения вероятности 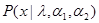, где 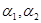- две совокупности параметров, первая из которых полностью неизвестна, а вторая стати­стически связана с совокупностью параметров , так что она подчиняет­ся распределению вероятности с плотностью 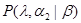, зависящей от третьей совокупности неизвестных параметров 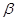. Представляя 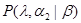в виде

,

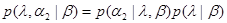где 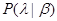- плотность распределения вероятности , заданная с точ­ностью до совокупности параметров 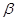, и выполняя интегрирование по получаем плотность распределения вероятности

,

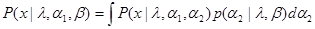которая зависит от 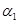и 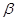. Обозначив совокупность этих параметров через 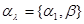, получим стандартное представление для функции прав­доподобия 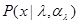, где совокупность параметров 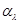включает в себя и параметры 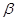, от которых зависит плотность 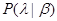априорного распре­деления вероятности.

Приведем другой пример более конкретного вида. Пусть 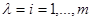, то есть принимает дискретные значения с вероятностями 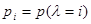, и величины 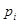неизвестны. Тогда 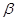- совокупность параметров 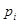( 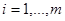), подчиненных ограничениям 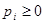, 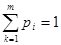. Пусть также совокупность данных наблюдения х есть 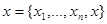, где ве­личины 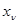( 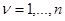)и х взаимно независимы, распределение веро­ятности величины х зависит от и имеет условную плотность вероятности

,

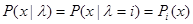авеличины 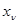не зависят от и имеют плотность распределения вероятности

,

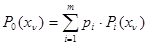где 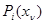- те же функции, что и выше, а 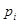- те же значения вероятностей, которые описывают распределение параметра . Полная совокупность данных наблюдения 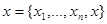имеет плотность распределения вероятности

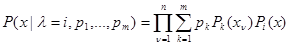
изависит от совокупности параметров 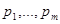,а плотность априор­ного распределения вероятности для

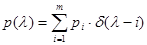
зависит от совокупности тех же параметров, то есть в данном случае

,

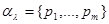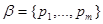
и обе совокупности полностью совпадают.

Приведенные примеры иллюстрируют возможности параметрическо­го описания априорной неопределенности и богатство возникающих при этом возможностей.

Параметрическое описание является удобным средством для учета имеющихся качественных представлений о статистическом поведении наблюдаемых данных х и параметров в сочетании с незнанием де­тальных количественных характеристик, точно определяющих это опи­сание. Именно такое сочетание наиболее характерно для большинства прикладных задач. Качественные представления, основанные на физи­ческой сущности рассматриваемой задачи, дают возможность задать структуру распределений вероятности для х и , а параметры 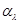и 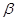сосредоточивают в себе имеющуюся неопределенность, не допускающую дальнейшую детализацию и уточнение качественной структуры. В роли параметров 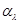и 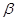в практических задачах могут выступать интенсивности полезных сигналов, несущих информацию о , и сопровождающих их помех, времена корреляции, характеристики объектов управления, параметры аппроксимирующих функций или дифференциальных урав­нений, используемых при описании процессов 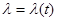и т. п. При пара­метрическом описании можно использовать также идеи прямых вариационных методов, вводя распределения 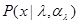и 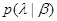в виде обрывков рядов по какой-либо полной системе известных функций. По­следнее дает возможность использовать параметрическое описание фор­мально, расширяя границы его применения на те случаи, когда апел­ляция к физическому содержанию задачи затруднительна.

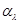Наконец, если х или имеют конечное множество значений, то в качестве параметров и 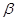можно рассматривать сами неизвестные вероятности этих значений. Таким образом, параметрическое описание априорной неопределенности является достаточно универсальным сред­ством учета ограниченных априорных сведений.

Это описание должно удовлетворять двум подчас противоречивым требованиям. Во-первых, оно должно качественно правильно и по воз­можности количественно точно отражать наши ограниченные априор­ные знания, так чтобы распределения с плотностям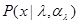и и 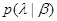действительно представляли при каких-нибудь 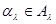и 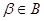возможные в данной задаче распределения. Во-вторых, число параметров не должно быть слишком велико. Увеличение размерности при­водит к ухудшению качества решения основной задачи как из-за слож­ности технической реализации алгоритмов обработки данных наблюде­ния х, так и из-за утраты некоторой доли входной информации, кото­рую неизбежно приходится затрачивать для определения значений или исключения неизвестных мешающих параметров. Поэтому синтезируе­мую в условиях априорной неопределенности систему целесообразно до­полнять алгоритмом проверки правильности априорных предположений, положенных в основу принятого в данной задаче параметрического опи­сания. Задача такого алгоритма - установить, верно ли качественно введенное описание (например, при фильтрации процесса 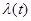- соот­ветствует ли действительности аппроксимация 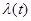полиномом заданной степени с неизвестными коэффициентами или эта модель неудовлетво­рительна) и достаточно ли числа введенных параметров. Такой алго­ритм дает возможность при необходимости усложнить параметрическое описание, увеличив число параметров или качественно изменив модель априорной неопределенности.

Введение дополнительных «мешающих» параметров при задании функции правдоподобия для описания неопределенности статистических свойств данных наблюдения х является традиционным для тех разделов математической статистики, которые имеют дело со статистическими выводами и принятием решений. Этим способом получены весьма суще­ственные результаты, в особенности применительно к задаче проверки сложных статистических гипотез, где удалось получить ряд строгих ре­зультатов. Этот подход широко использован при синтезе при­ближенно оптимальных систем обработки информации более широкого класса.