Изучение связей между качественными показателями
Качественные признаки (пол, образование, профессия работников, форма собственности предприятий и т.д.), взаимосвязи между ними , их влияние на другие показатели (в том числе и количественные) особенно часто приходится изучать при проведении различных социологических исследований путем опроса или анкетирования. Если признаки показателей атрибутивные, для изучения связей используют комбинационное распределение единиц совокупности по двум (и более) признакам, оформляемое в виде таблиц сопряженности.
Для измерения тесноты связи между группировочными признаками в таблицах взаимной сопряженности используют такие показатели, как коэффициент ассоциации Кас, коэффициент контингенции Кконт, коэффициенты взаимной сопряженности Пирсона и Чупрова. Первые два применяются лишь для «четырехклеточных» таблиц, а последние – для любой размерности. Частоты в первых можно обозначить через a,b,c,d .
Рассмотрим такую таблицу связи «четырех полей» (табл. 2.4 из [16, c.213]) и рассчитаем соответствующие коэффициенты.
В условном примере приведены данные о распределении 500 опрошенных человек по двум показателям: наличие (отсутствие) прививки от гриппа и факт заболевания (незаболевания) гриппом во время эпидемии.Не трудно заметить , что среди сделавших прививку 90 % не заболели гриппом, а среди не сделавших 60 % заболели. Можно предположить , что прививка положительно влияет на предупреждение заболевания и существует статистическая зависимость между группировочными признаками. Это суждение можно подкрепить статистическими критериями, например критерием Пирсона 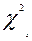 , и приведенными выше коэффициентами .
, и приведенными выше коэффициентами .
Коэффициент ассоциации выражается формулой:
Кас= 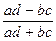 =
= 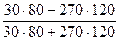 = - 0.862.
= - 0.862.
Таблица 2.4
Таблица четырех полей
| группы лиц | Число лиц | ||
| Заболевших гриппом | Не заболевших гриппом | Итого | |
| Сделавших прививку | 30 (a) | 270 (b) | |
| Не сделавших прививку | 120 (c) | 80 (d) | |
| Итого | |||
| Теоретические значения числа лиц | |||
| Группа | I (да) | II (нет) | ∑ |
| I (да) | 30 (90) | 270 (210) | |
| II (нет) | 120 (60) | 80 (140) | |
| ∑ |
Коэффициент контингенции выражается формулой:
Кконт = 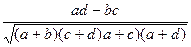 =
= 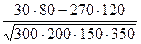 = - 0,534.
= - 0,534.
Связь считается достаточно значительной и подтвержденной, если 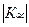 > 0,5 или
> 0,5 или 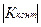 >0,3. Поэтому в нашем примере оба коэффициента характеризуют достаточно большую обратную зависимость между прививками и заболеванием.
>0,3. Поэтому в нашем примере оба коэффициента характеризуют достаточно большую обратную зависимость между прививками и заболеванием.
Чтобы использовать критерий Пирсона, в таблице взаимной сопряженности наряду с эмпирическими частотами (или частостями) записывают теоретические частоты, рассчитываемые исходя из нулевой гипотезы, то есть в предположении, что зависимость между признаками отсутствует. При этом теоретические частоты (частости) по строкам (или графам) рассчитывают пропорционально распределению единиц в итоговой строке (или графе). Например, в итоговой строке доля заболевших 0, 3 (не заболевших-0,7). Соответственно в переписанной таблице (нижние строки) теоретические частоты представлены рядом с эмпирическими в скобках.
Критерий Пирсона 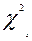 рассчитывается по формуле:
рассчитывается по формуле:
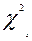 =
= 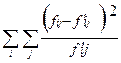 или
или 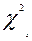 =
= 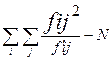 ,
,
где N =∑ 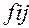 - общее число единиц совокупности;
- общее число единиц совокупности;
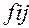 - эмпирические частоты по группам;
- эмпирические частоты по группам;
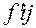 - теоретические частоты по группам. Подставив соответствующие данные из таблицы 2.7, получим:
- теоретические частоты по группам. Подставив соответствующие данные из таблицы 2.7, получим:
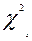 =
= 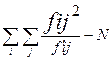 = (302/90 + 2702/210 +1202/60 + 802/140) - 500 =142,85.
= (302/90 + 2702/210 +1202/60 + 802/140) - 500 =142,85.
Рассчитанное (фактическое) значение 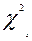 сравнивается с табличным, определяемым по таблице приложения 4 [16] для заданного уровня значимости α и числа степеней свободы ύ = (k1-1)(k2-1), где k1 и k2 – число групп по признакам группировки (число строк и граф в таблице).
сравнивается с табличным, определяемым по таблице приложения 4 [16] для заданного уровня значимости α и числа степеней свободы ύ = (k1-1)(k2-1), где k1 и k2 – число групп по признакам группировки (число строк и граф в таблице).
В рассматриваеиом примере ύ = (2-10)(2-1) = 1. Приняв уровень значимости α = 0.05, по Приложению 4 [16] находим 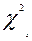 табл = 3,84. Так как
табл = 3,84. Так как 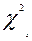 факт >
факт > 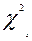 табл , то выдвинутая нулевая гипотеза отвергается, а это значит, что существует статистическая зависимость между наличием прививки и заболеванием гриппом.
табл , то выдвинутая нулевая гипотеза отвергается, а это значит, что существует статистическая зависимость между наличием прививки и заболеванием гриппом.
Аналогично рассчитываются теоретические частоты и критерий Пирсона 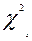 и в таблицах взаимной сопряженности большей размерности.
и в таблицах взаимной сопряженности большей размерности.
Коэффициент взаимной сопряженности Пирсона рассчитывается на основе показателя 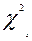 по формуле:
по формуле:
Кп = С = 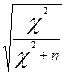 =
= 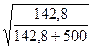 = 0,46.
= 0,46.
Коэффициент взаимной сопряженности Чупрова также рассчитывается на основе показателя 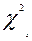 по формуле:
по формуле:
Кч = 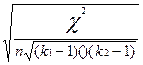 =
= 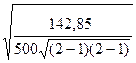 = 0,53,
= 0,53,
где n - число единиц наблюдения;
k1 и k2-соответственно число строк и столбцов в таблице.
Итак, на основе метода группировок с помощью коэффициентов может быть измерена теснота связей и между качественными показателями.
Для измерения тесноты связи применяются:
- линейный коэффициент корреляции;
- теоретическое корреляционное отношение;
- индекс корреляции.
Дата добавления: 2020-10-25; просмотров: 589;











