I. Изучение нового материала.

Определения и понятия дифференциальных уравнений

Дифференциальное уравнение –основной математический аппарат в естествознании. Они применяются в физике, астрономии, аэродинамике и теории упругости, химии, экономике, биологии и медицине. Такой подход к изучению явлений природы впервые был предложен итальянским ученным Г. Галилеем. Впервые его блестяще применил один из создателе математического анализа И. Ньютон.

Решение задач методом математического моделирования сводится к отысканию неизвестной функции из уравнения, содержащего независимую переменную, искомую функцию и производные этой функции.

Определение.Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную x, искомую функцию y и ее производные или дифференциалы.

Определение.Решением дифференциального уравнения называется всякая функция, которая обращает данное уравнение в тождество.

Существуют задачи, приводящие к дифференциальным уравнениям. Рассмотрим одну из них.

1. Размножение бактерий.На опытах с бактериями установлено, что скорость размножения бактерий пропорциональна их количеству, если, конечно, для них имеется достаточный запас пищи.

Так как сами бактерии очень малы, а их количество велико, то можно считать, что масса бактерий с течением времени меняется непрерывно. Тогда скорость прироста массы бактерий называется скоростью размножения.

Если через число x(t) обозначить массу всех бактерий в момент времени t, то 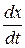будет скоростью размножения этих бактерий. Так как скорость размножения 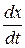пропорциональна количеству бактерий, то существует постоянная k такая, что

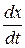= kx. (1)

По условию x(t) и x^/(t) неотрицательные, поэтому коэффициент k тоже неотрицательный.

Уравнение (1) является простейшим примером дифференциального уравнения. Оно называется дифференциальным уравнением размножения. Искомым неизвестным уравнения (1) является функция x = x(t), которая в уравнение входит вместе со своей производной.

Решением данного уравнения является функция вида

x = Ce^kt, где С – const.

Действительно,

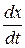=(Ce^kt) =С∙ e^kt ∙ k = k(Ce^kt) = kx.

2. Задача 1. Найти закон движения тела по оси Ox, если оно начало двигаться из точки М(4;0) со скоростью v = 2t + 3t².

При прямолинейном движении скорость есть производная от пути по времени. Обозначим путь через x, имеем v = 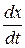;тогда 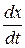= 2t + 3t². Получили дифференциальное уравнение.

3. Радиоактивный распад.Опытом установлено, что скорость распада радия в каждый момент времени пропорциональна начальному количеству радия.

Таким образом, если через x(t) обозначить массу вещества, еще не распавшегося к моменту времени t, то скорость распада 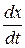удовлетворяет уравнению: 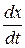= - kx(t), где k – некоторая положительная постоянная. . Знак минус показывает, что x(t) – убывающая функция, следовательно 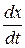< 0.

Уравнение 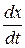= - kx(t)называется дифференциальным уравнением радиоактивного распада.