Корреляционное отношение
Согласно правилу сложения дисперсий, общая дисперсия равна сумме средней из групповых и межгрупповой дисперсий:

Зная общую и межгрупповую дисперсии, можно оценить долю, которую составляет вариация под действием фактора в общей вариации результативного признака , т.е. найти отношение дисперсий
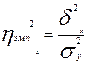
Эмпирическое корреляционное отношение определяется как корень из этого отношения дисперсий:

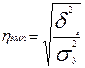
где σ2 –общая дисперсия,
δ2 - межгрупповая дисперсия,
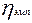 – эмпирическое корреляционное отношение.
– эмпирическое корреляционное отношение.
Корреляционное отношение равно нулю, когда нет колеблемости в величине средних значений результативного признака по выделенным группам. В тех случаях, когда средняя из групповых дисперсий близка к нулю, т.е. практически вся вариация результативного признака обусловлена действием фактора , величина корреляционного отношения близка к 1.
Теоретическое корреляционное отношение (индекс корреляции)применяется для измерения тесноты корреляционной связи между признаками при любой форме связи, как линейной, так и нелинейной. Данный показатель можно вычислять только после того, как определена теоретическая линия регрессии.Теоретическое корреляционное отношение рассчитывается на основе выравненных (теоретических) значений результативного признака 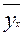 (по уравнению регрессии). Теоретическое корреляционное отношение представляет собой относительную величину, получаемую в результате сравнения среднего квадратического отклонения в ряду теоретических значений результативного признака со средним квадратическим отношением в ряду эмпирических значений (или корень квадратный из отношения дисперсий теоретического и эмпирического ряда значений результативного признака). Оно рассчитывается по формуле:
(по уравнению регрессии). Теоретическое корреляционное отношение представляет собой относительную величину, получаемую в результате сравнения среднего квадратического отклонения в ряду теоретических значений результативного признака со средним квадратическим отношением в ряду эмпирических значений (или корень квадратный из отношения дисперсий теоретического и эмпирического ряда значений результативного признака). Оно рассчитывается по формуле:
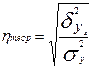
где 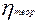 - теоретическое корреляционное отношение;
- теоретическое корреляционное отношение;
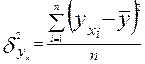 - факторная дисперсия, которая характеризует вариацию результативного признака под влиянием признака-фактора.
- факторная дисперсия, которая характеризует вариацию результативного признака под влиянием признака-фактора.
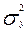 - общая дисперсия, показывающая вариацию результативного признака под влиянием всех факторов, вызывающих эту вариацию. Отношение факторной дисперсии к общей дисперсии называется теоретическим коэффициентом детерминации
- общая дисперсия, показывающая вариацию результативного признака под влиянием всех факторов, вызывающих эту вариацию. Отношение факторной дисперсии к общей дисперсии называется теоретическим коэффициентом детерминации 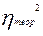 :
:
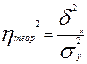 .
.
 Теоретический коэффициент детерминации показывает, какую долю в общей дисперсии результативного признака занимает дисперсия, выражающая влияние вариации фактора x на вариацию y. В основе исчисления и эмпирического и теоретического корреляционного отношения лежит правило сложения дисперсии, согласно которому в первом случае общая дисперсия равна сумме межгрупповой дисперсии и средней из групповых, то есть . Во втором случае в качестве межгрупповой дисперсии выступает дисперсия теоретических значений результативного признака, которую можно назвать факторной
Теоретический коэффициент детерминации показывает, какую долю в общей дисперсии результативного признака занимает дисперсия, выражающая влияние вариации фактора x на вариацию y. В основе исчисления и эмпирического и теоретического корреляционного отношения лежит правило сложения дисперсии, согласно которому в первом случае общая дисперсия равна сумме межгрупповой дисперсии и средней из групповых, то есть . Во втором случае в качестве межгрупповой дисперсии выступает дисперсия теоретических значений результативного признака, которую можно назвать факторной 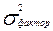 , поскольку она отражает влияние фактора x на вариацию y. А вместо средней из групповых дисперсий принимается остаточная дисперсия
, поскольку она отражает влияние фактора x на вариацию y. А вместо средней из групповых дисперсий принимается остаточная дисперсия 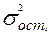 , отражающая влияние на вариацию на вариацию результативного признака всех остальных факторов (кроме x), не учтенных в модели (в уравнении регрессии).Таким образом , общая дисперсия эмпирического ряда y равна сумме факторной и и остаточной дисперсий:
, отражающая влияние на вариацию на вариацию результативного признака всех остальных факторов (кроме x), не учтенных в модели (в уравнении регрессии).Таким образом , общая дисперсия эмпирического ряда y равна сумме факторной и и остаточной дисперсий:
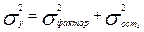 ,
,
а теоретическое корреляционное отношение будет исчисляться по формуле:
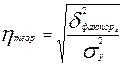 .
.
Факторную дисперсию можно выразить как разность 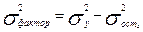 .
.
Если ввести в формулу остаточную дисперсию, которая характеризует вариацию результативного признака под влиянием прочих неучтенных факторов
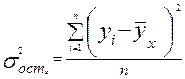 ,
,
то получим
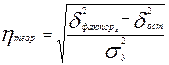 или
или 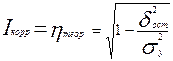 .
.
В последнем виде корреляционное отношение при криволинейной форме связи называется индексом корреляции I корр.
Индекс корреляции может находиться в пределах от 0 до 1.
Если результативный признак всецело зависит от фактора x (т.е. связь функциональная), то выравненные (теоретические) значения 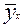 совпадают с эмпирическими y. Тогда
совпадают с эмпирическими y. Тогда 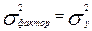 , или
, или 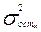 =0 и корреляционное отношение
=0 и корреляционное отношение 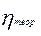 =1, что означает полную зависимость вариации y от вариации x. Если же фактор x не оказывает никакого влияния на вариацию y, то общая дисперсия
=1, что означает полную зависимость вариации y от вариации x. Если же фактор x не оказывает никакого влияния на вариацию y, то общая дисперсия 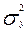 совпадает с остаточной
совпадает с остаточной 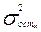 , то есть
, то есть 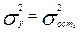 . И в этом случае
. И в этом случае 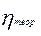 = 0. Это означает, что признак y не коррелирован с фактором x.
= 0. Это означает, что признак y не коррелирован с фактором x.
Чем ближе значения 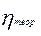 к 1, тем теснее связь между вариацией x и y. И наоборот, , чем ближе
к 1, тем теснее связь между вариацией x и y. И наоборот, , чем ближе 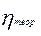 к 0, тем зависимость слабее. Считается, что если
к 0, тем зависимость слабее. Считается, что если 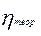 < 0,3, то зависимость малая;
< 0,3, то зависимость малая;
0,3 < 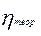 < 0,6 - зависимость средняя;
< 0,6 - зависимость средняя;
0,6 < 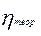 < 0,8 - зависимость выше средней;
< 0,8 - зависимость выше средней;
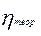 .> 0,8 - зависимость большая.
.> 0,8 - зависимость большая.
Рассмотрим корреляционную связь на условном примере параболы 2-го порядка, отражающей зависимость между урожайностью озимой пщеницы в ц/ га (y) и количеством внесенных органических удобрений в т/га (x) [16, c. 250-253 и c. 260-261] и рассчитаем индекс корреляции (табл.2.10, 2.10-1).
Таблица 2.10
Расчетная таблица для определения параметров параболы 2-го порядка
| x | y | x2 | x3 | x4 | xy | x2y | 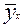
|
| 16,2 | |||||||
| 18,5 | |||||||
| 20,4 | |||||||
| 21,9 | |||||||
| 23,0 | |||||||
| ∑ 15 |
Уравнение параболы имеет вид:
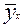 =a0 + a1x + a2x2.
=a0 + a1x + a2x2.
Параметры найдем по методу наименьших квадратов, для чего используем систему нормальных уравнений:
na0 + a1∑x + a2∑x2 = ∑y,
a0∑x + a1∑x2 + a2∑x3 =∑xy,
a0∑x2 + a1∑x3 + a2∑x4 = ∑x2y.
По данным таблицы 2.6 ( графы 1-7) система уравнений запишется:
5a0 + 15a1 + 55a2 = 100,
15a0 + 55a1 + 225a2 =317,
55a0 + 225a1 + 979a2 = 1199.
Решив эту систему, получим:
a0 =13,41, a1 =2,98, a2 = - 0,214.
Отсюда искомое уравнение
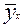 =13,41+ 2,98x – 0,214x2.
=13,41+ 2,98x – 0,214x2.
Подставив в это уравнение значения x (графа 1) получаем теоретические значения результативного показателя 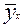 (графа 8).
(графа 8).
Для расчета теоретического корреляционного отношения (индекса корреляции) построим таблицу 2.10-1, взяв исходные данные (графы 1-3) из таблицы 2.10 (графы 1,2. 8).
Общая средняя урожайность равна (графа2, графа 3):
 =
= 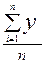 = 100/5 = 20 ц / га.
= 100/5 = 20 ц / га.
Общая дисперсия рассчитывается по формуле (данные в графе 5):
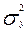 =
= 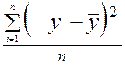 = 30/5 = 6.
= 30/5 = 6.
Таблица 2.10-1
Расчетная таблица для нахождения корреляционного отношения.
| X | Y | 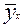
| y- 
| (y-  )2 )2
| 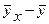 ) )
| 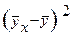
| y- 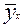
| (y- 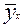 )2 )2
|
| 16,2 | -4 | -3,8 | 14,44 | -0,2 | 0,04 | |||
| 18,5 | -1 | -1,5 | 2,25 | 0,5 | 0,25 | |||
| 20,4 | 0,4 | 0,16 | -0,4 | 0,16 | ||||
| 21,9 | 1,9 | 3,61 | 0,1 | 0,01 | ||||
| 23,0 | 3,0 | 9,00 | ||||||
| ∑ 15 | 29,46 | 0,46 | ||||||
| Средн. | 5,892 | 0,077 |
Факторная дисперсия рассчитывается по формуле (данные в графе 7).
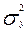 =
= 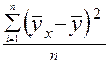 = 29,46 / 5 = 5,892.
= 29,46 / 5 = 5,892.
Отсюда теоретическое корреляционное отношение равно:
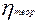 =
= 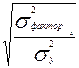 =
= 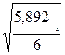 = 0,99.
= 0,99.
Полученное значение 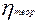 =0,99 характеризует очень тесную зависимость изменения урожайности от изменения количества внесенных удобрений.
=0,99 характеризует очень тесную зависимость изменения урожайности от изменения количества внесенных удобрений.
Такой же результат получим, используя формулу индекса корреляции. Данные для остаточной дисперсии 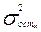 рассчитаны в графе 9 табл.2.10-1. Остаточная дисперсия равна:
рассчитаны в графе 9 табл.2.10-1. Остаточная дисперсия равна:
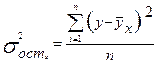 = 0,46/6 = 0,077.
= 0,46/6 = 0,077.
Отсюда
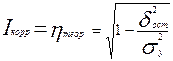 =
= 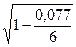 = 0,99.
= 0,99.
Дата добавления: 2020-10-25; просмотров: 1356;











