Уравнение регрессии
Определение формы связи и отыскание параметров уравнения называется нахождением уравнения связи (уравнения регрессии). Найти уравнение регрессии – значит по эмпирическим данным математически описать изменения взаимно коррелируемых величин. Уравнение регрессии можно рассматривать как вероятностную гипотетическую функциональную связь средней величины результативного признака y со значениями факторного признака x или теоретическую линию регрессии. Рассчитанные по уравнению значения результативного признака называются теоретическими (обозначаются 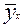 ).
).
Для характеристики связей экономических показателей используют следующие типы функций:
- линейную 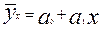

- гиперболическую ;

- степенную ;
Таблица 2.6
Значения tтабл
  k = n-2
k = n-2
| α = 0,5 2,10 | α=0,01 2,88 |
| 2,09 | 2,86 | |
| 2,09 | 2,85 | |
| 2,08 | 2,83 | |
| 2,07 | 2,82 | |
| 2,07 | 2,81 | |
| 2,06 | 2,80 | |
| 2,06 | 2,79 | |
| 2,06 | 2,78 | |
| 2,05 | 2,76 | |
| 2,05 | 2,76 | |
| 2,04 | 2,75 | |
| 2,02 | 2,70 | |
| 2,00 | 2,66 | |
| 1,98 | 2,62 | |
| 1,96 | 2,58 |

- показательную ;

- параболическую ;

- логарифмическую ;

- логистическую .
Параметры уравнений связи определяют из так называемой системы нормальных уравнений, отвечающих требованию метода наименьших квадратов (МНК). Это требование можно записать как 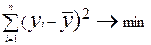 , то есть требуется определить, при каких значениях параметров сумма квадратов отклонений y от
, то есть требуется определить, при каких значениях параметров сумма квадратов отклонений y от 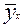 будет минимальной.
будет минимальной.
Необходимым условием экстремума является равенство нулю частных производных по параметрам. Приравнивая к нулю частные производные функции по параметрам, получим систему линейных уравнений для нахождения параметров по имеющимся эмпирическим данным:
При линейной зависимости она имеет вид:

Необходимые для решения данной системы показатели (суммы) определяются по наблюдаемым эмпирическим данным. Параметр a1 называется коэффициентом регрессии. Он показывает, на сколько в абсолютном выражении изменится результативный показатель y при изменении факторного показателя x на единицу.
Рассмотрим расчет параметров уравнения регрессии на примере, исходные данные по которому приведены в табл.2.7 (графы 1, 2). Они соответствуют данным, приведенным в табл.2.1 (графы 2, 3).
Таблица 2.7.
Расчетная таблица для определения параметров уравнения регрессии по индивидуальным данным
| Основные производственные фонды, млн.руб. xi | Валовый вы-пуск продук-ции, млн. руб. yi | x2 | xy |
|
| ∑520 | ∑y =1000 | ∑ x2 =35624 | ∑xy = 70244 | ∑ 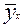 = 1000 = 1000
|
| Средние | ||||
Решение
Заполним графы 3-4 таблицы 2.7, рассчитав соответствующие произведения и просуммировав их. Подставив найденные суммы в систему нормальных уравнений получим:
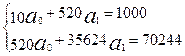
Решив полученную систему уравнений, найдем, что а0 = -10,24, а1 = 2,12. Коэффициент регрессии, равный а1 = 2,12, показывает, что при изменении объема основных фондов (факторного показателя x) на 1 млн. руб. валовый выпуск продукции (результативный показатель y) увеличится на 2,12 млн. руб..
Отсюда искомое уравнение 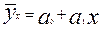 = будет
= будет
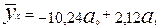 .
.
Подставив в данное уравнение последовательно значения х (12,16, 25 и т.д.), находим 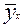 (графа 5 табл.2.5). Его можно использовать и для прогноза. Например, если объем фондов будет 120 млн руб.,то объем выпуска можно ожидать 244 млн.руб.(см последнюю строку).
(графа 5 табл.2.5). Его можно использовать и для прогноза. Например, если объем фондов будет 120 млн руб.,то объем выпуска можно ожидать 244 млн.руб.(см последнюю строку).
Для расчет параметров уравнения по сгруппированным данным строят аналитическую или корреляционную таблицы, где указаны распределения по x и y и, соответственно, их частоты fx и fy. При этом ∑fx = ∑fy = n. Поэтому система нормальных уравнений для расчета параметров линейного уравнения регрессии будет иметь вид:
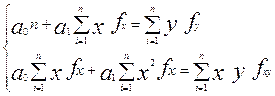
Рассмотрим расчет параметров уравнения регрессии по данным корреляционной таблицы на примере, исходные данные по которому приведены в табл.2.8 . Они соответствуют данным, приведенным в табл.2.3. Дополнительно созданные три столбца (графы 7-9) и 2 строки внизу позволяют получить все необходимые суммы для расчета параметров.
Подставив полученные суммы в систему уравнений, имеем:
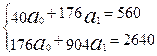
Решив систему, находим параметры: a0 = 8,06, a1 = 1,35. Искомое уравнение будет:
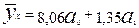
По данным корреляционной таблицы легко рассчитать и линейный коэффициент корреляции по формуле:
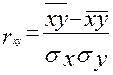 .
.
Таблица 2.8
Расчетная таблица нахождения параметров уравнения регрессии по сгруппированным данным
| Значение признака xi | Значение признака yi | Итого fx = fj | xfx | x2fx | xyfxy | |||
| - | - | |||||||
| - | ||||||||
| - | ||||||||
| - | - | |||||||
| Итого (число единиц fy =fi | ∑fj = 40 | |||||||
| yf | ∑yfy= 560 |  =14 =14
| ||||||
| y2fy | ∑y2fy= | 212,5 | ||||||
| Cредние | 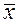 =4,4 =4,4
| 22,6 |
Все средние арифметические (числитель ) приведены в таблице, а необходимые среднеквадратические отклонения найдем по формулам:
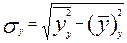 =
=  = 1,8
= 1,8
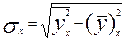 =
= 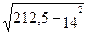 = 4,06.
= 4,06.
Отсюда r = 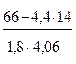 = 0,6. То есть, между производительностью труда y и стажем работников x связь cредняя( умеренная).
= 0,6. То есть, между производительностью труда y и стажем работников x связь cредняя( умеренная).
Рассмотрим решение некоторых задач корреляционно-регрессионного анализа по теме на примере, приведенном в [1, c. 95-96].
Пусть по 10 однотипным предприятиям имеются следующие данные о выпуске продукции (x) и о расходе условного топлива (y) в тоннах (графы 1 и 2 таблицы 2.9):
Таблица 2.9.
Расчет показателей корреляционно-регрессионного анализа
| X | Y | x2 | Xy | yx = 1,16 +0,547 x | y2 |
| 3,9 | |||||
| 4.4 | |||||
| 5.5 | |||||
| 5.5 | |||||
| 6.6 | |||||
| 6.6 | |||||
| 8.8 | |||||
| 12.1 | |||||
| 12.1 | |||||
| 14.3 | |||||
| 12,5 | 8,0 | 196,1 | 121,8 | 8,0 | 77,0 |
Требуется найти уравнение зависимости расхода топлива от выпуска продукции (или уравнение регрессии y по x) и измерить тесноту связей между ними.
Решение представим в виде методики регрессинно- корреляционного анализа, раскрывающей их суть.
1. Построим уравнение регрессии в форме линейной функции вида yx = a0 + a1 x, параметры уравнения (a0 и a1) найдем из системы нормальных уравнений

1.1.Чтобы получить необходимые для решения показатели введем вспомогательные графы 3 и 4 (x2 и xy) таблицы и в итоговой строке таблицы поставим суммы ∑x, ∑y, ∑x2, ∑xy, рассчитанные путем суммирования всех элементов граф. Подставляем их в уравнения и решаем систему:
10 a0 + 125 a1 = 80,
125 a0 +1961a1 = 1218,

a1 = (10*1218-125*80): (10*1961- 1252 ) = 2180:3985 = 0,547
a0 = (80:10)- 0,547*125: 10 = 8- 6,84 = 1,16
Отсюда yx = 1,16 +0,547 x.
Подставляя в это уравнение последовательно значения x = 5, 6, 8, 10 и т. д., получаем выравненные (теоретические) значения результативного показателя yx (графа 5 таблицы). Величина суммы по графе 5 должна быть близка к сумме по графе 2 (отличаться только за счет округлений при расчетах), так как по МНК отклонения должны взаимно погаситься по свойству средней арифметической. Сумма выравненных значений в графе 5 (80) точно равна сумме эмпирических значений в графе 2 (80), что свидетельстует о возможности аналитического выравнивания по прямой зависимости.
1.2. Для измерения тесноты связи между y и x рассчитаем линейный коэффициент корреляции по самой простой формуле:
rxy 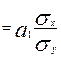
Для расчета дисперсии по y введем вспомогательную графу 6 таблицы (у2) и дополнительную строку средних величин, полученную делением всех сумм на n (10). Находим 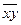 =121,8;
=121,8;  =12,5;
=12,5;  =8;
=8; 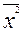 =196,1,
=196,1, 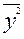 = 77,0.
= 77,0.
Используя простейшую формулу расчета дисперсии и данные строки средних получим:
(σx)2= 196.1 – 12.52 = 196,1 – 156,25 = 39,85; σx = 6,31.
(σy)2 = 77 - 82 = 13; σy = 3,6.
rxy = 0,547* 6,31 : 3,6 = 0,96.
Значение линейного коэффициента корреляции (0,96), близкое к единице, характеризует не только меру тесноты зависимости вариации y от вариации x, но и степень близости этой зависимости к линейной.
Аналогичный результат можно получить и по формуле

Подставив все имеющиеся в таблице показатели, получим
rxy = (121,8 - 12.5*8) : (6,31*3,6) = 21,8 : 22,716 = 0,96
Для оценки значимости (существенности) линейного коэффициента необходимо его сопоставить со средней квадратической ошибкой (σr).Для n <30 значимость коэффициента корреляции проверяется на основе t-критерия Стьюдента.
σr =(  ) : (
) : (  ) =(
) =( 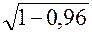 ): (
): ( 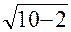 ) = 0,1
) = 0,1
tфакт = 0.96 : 0,1 = 9,6
По таблице Приложения 9 в [1, с. 199] находим, что при числе степеней свободы n-2 (8) и уровне значимости α = 0.05 табличное (критическое) значение tтабл равно 2.306. Поскольку tфакт > tтабл, то линейный коэффициент rxy = 0,96 считается значимым , а связь между x и y – реальной.
Следовательно, между выпуском продукции х и расходом условного топлива y в данном примере существует прямая линейная связь, близкая к функциональной.
Выполнить корреляционный и регрессионный анализ можно на персональном компьютере по пакетам прикладных программ Excel, Eviews, Statgraphics и другим. Подробно методика их использования и примеры рассмотрены в [10, c.98-99, 14, с.191-218].
Для данного примера методика расчета по программам парной линейной регрессии с помощью Microsoft Office Excel 2007 включает следующие действия [10, c. 98]:
1. Выбрать Данные- Анализ данных – Регрессия
2. В диалоговом окне Регрессия сделать следующее:
- ввести в окне редактирования Входной интервал Y диапазон зависимой переменной;
- ввести в окне редактирования Входной интервал X диапазон зависимой переменной;
- установить флажок Метки, если первая строка содержит названия столбцов;
- установить флажок Константа –ноль, если в уравнении регрессии отсутствует свободный член a;
- ввести в окне редактирования Выходной интервал номер свободной ячейки на рабочем листе;
- Нажать кнопку ОК.
При криволинейной зависимости линейный коэффициент корреляции недооценивает степень тесноты связи и даже может быть равен 0, а потому в таких случаях рекомендуется использовать в качестве показателя степени тесноты связи другие величины.
Дата добавления: 2020-10-25; просмотров: 645;











