Параллельное рассмотрение значений x и y в каждой из n единиц

При небольшом числе наблюдений наличие корреляционной связи между двумя призаками можно выявить путем простого параллельного сравнения их значений у отдельных единиц. Для этого единицы наблюдения располагают по возрастанию значения факторного признака x и рассматривают поведение значений результативного показателя у. Примером может служить приведенные в таблице условные показатели деятельности 10 предприятий (табл.2.1).

Из таблицы видно, что по мере увеличения значений x увеличиваются и значения y (исключение- 3 и 7 предприятия). В целом же можно сказать, что с ростом объемов основных фондов растет и валовой выпуск продукции предприятий.

Такой вывод о наличии связей обычно сопровождается расчетом других показателей, используемых для измерения направления и тесноты связей: коэффициента Фехнера, ранговых коэффициентов корреляции, линейного коэффициента корреляции.

Коэффициент Фехнера (коэффициент корреляции знаков) основан на сравнении поведения отклонений индивидуальных значений каждого признака от своей средней величины (табл.2.1, графы 4, 5).При этом во

Таблица 2.1.

Показатели деятельности предприятий

Пред-приятия	Основные производственные фонды, млн.руб.	Валовый выпуск продукции, млн. руб.	Знаки отклонений
xi	yi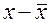
			-	-
			-	-
			-	-
			-	-
			-	-
			+	+
			+	-
			+	+
			+	+
			+	+
∑
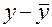
Средние

внимание принимаются только знаки отклонений («+»), («-». Определив знаки, рассматривают все пары знаков и подсчитывают число их совпадений С и несовпадений Н. При таких обозначениях коэффициент Фехнера К_ф равен:

К_ф = ,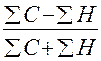

то есть, коэффициент Фехнера равен отношению разности чисел пар совпадений и несовпадений знаков к их сумме. Как и любой показатель тесноты связей, коэффициент Фехнера может принимать значение от 0 до 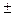1. При этом чем ближе значение к единице, тем больше (теснее) зависисмость между между x и y.

В нашем примере число совпадений составило (табл.2.1, графы 4, 5) 9, а число несовпадений – 1.

К_ф = 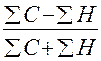= (9-1)/ (9+1) = 0,8.

Такое значение свидельствует о сильной зависимости. Однако, так как К_ф не учитывает величину отклонений (только знаки), он практически характеризует не столько тесноту связей, сколько ее наличие и направленность. В примере по значению и знаку (+) К_ф можно сказать, что между x и y существует прямая корреляционная связь.

Корреляционную связь между x и y для наглядности можно изобразить графически. Для этого, пользуясь прямоугольной системой координат (х- по оси абцисс и y – по оси ординат) каждую пару изображают точкой на плоскости. Соединяя последовательно нанесенные точки, получают ломаную линию, называемую эмпирической линией регрессии.