Коэффициенты корреляции рангов

Для измерения тесноты связей часто используются простые по расчету непараметрические показатели, к числу которых, кроме коэффициента Фехнера, относятся коэффицициенты корреляции рангов Спирмэна (ρ) и Кендэла ( ).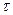

Ранг –это порядковый номер, присваиваемый каждому индивидуальному значению x и y (отдельно) в ранжированном ряду. Нумерация их чаще всего от 1 до n по возрастанию значений признака (или наоборот по убыванию). Ранги признаков x и y обозначают символами N_x и N_y. Суждение о связи между изменениями значений х и у основано на сравнении поведения рангов по двум признакам параллельно. Если у каждой пары x и y ранги совпадают, это характеризует максимально тесную прямую связь. Если наоборот, то есть в одном ряду ранги возрастают от 1 до n, а в другом – убывают от n до 1, это максимально возможная обратная связь.

Для расчета коэффициента Спирмэна значения признаков x и y нумеруют (отдельно) в порядке возрастания от 1 до n, то есть им присваивают определенный ранг (N_x и N_y) - порядковый номер в ранжированном ряду. Затем для каждой пары рангов находят их разность ( d = N_x - N_y), и квадраты этой разности суммируют. Коэффициент корреляции рангов Спирмэна рассчитывают по формуле:

ρ=1- (6∑d2)/(n³- n), или ρ = 1- .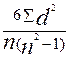

где d – разность рангов x и y;

n - число наблюдаемых пар значений x и y.

Коэффициент корреляции рангов Спирмэна может принимать значения от 0 до 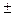1. Однако равенство 0 или 1 нельзя расценивать как отсутствие связей или свидетельство функциональной связи ( как в случае равенства 0 или 1 линейного коэффициента корреляции r), так как он учитывает разность только рангов (а не самих значений) x и y. Во всех остальных случаях он близок к r , и благодаря простоте расчета более предпочтителен, особенно на начальном этапе выявления наличия связи.

Расчет коэффициента Кендэла начинается также с ранжирования значений признаков x и y. Ранги x (N_x) располагают строго в порядке возрастания и параллельно записывают соотвествующие N_y. Для каждого N_y последовательно определяют число следующих за ним рангов, превышающих его значение, и число рангов, меньших по значению. Первые учитываются со знаком + и их сумма обозначается буквой Р, вторые учитываются со знаком – и их сумма обозначается буквой Q. Если ранги x и y совпадают и число пар равно n, то

Р_max = .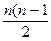

Если тенденция обратная, то Q будет иметь такое же максимальное значение по модулю:

= .

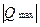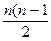Если же ранги y не совпадают с рангами x, то суммируются все положительные и отрицательные баллы (S = P+Q); отношение данной суммы S к максимальному значению одного из них и представляет собой коэффициент корреляции рангов Кендэла 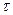, то есть

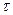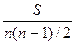= или .

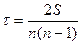Рассмотрим расчет коэффициентов корреляции рангов на условном примере данных о часовой оплате труда x и уровне текучести кадров y ( табл.2.8)[16,c.231].

В графах 1 и 2 приведены исходные значения x и y. В графах 3 и 4 поставлены ранги N_x и N_y, полученные путем ранжирования значений x и y в порядке возрастания, и параллельно записанные в соответствии с их значением по N_x. В графе 5 показаны разности рангов d = N_x –N_y, а в графе 6- значения квадратов этих разностей рангов, в итоговой строке по этой графе показана сумма, подставляемая в формулу. В результате расчета получаем:

ρ=1- (6∑d2)/(n3- n)= 1- [6*164: (8³- 8)] = 1-[ 984:504] =

= 1- 1,95 = - 0,95

Полученное значение коэффициента корреляции рангов Спирмэна

ρ= - 0,95) свидетельствует о сильной обратной связи между x и y.

В графах 7 и 8 приведедены баллы со знаком (+ ), то есть число следующих рангов, превышающих данный ранг (графа 7) и число рангров, меньших по значению (графа 8). Их итоги (P =2, Q = -26), необходимые для расчета коэффициента Кендэла, показаны в итоговой строке. Их сумма равна S= P + Q= 2 + (- 26) = - 24. Подставляем их в формулу получим:

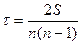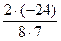= = - 0857.

Таблица 2.2

Расчет коэффициентов рангов Спирмэна и Кендэла

X	Y	Ранги	Показатели для расчета коэффициента Спирмэна ρ	Показатели для расчета коэффициента Кендэла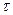
Nx	Ny	d	d2	«+»	«-»
				-6
				-6
				-3
				-1
						-	-
n=8					∑ d2=164	P=2	Q= -26

Полученное отрицательное значение коэффициента Кендэла

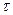= - 0857 также характеризует сильную обратную связь между x и y,

то есть между уровнем оплаты труда и текучестью кадров.

Метод группировок

При большом числе наблюдений для выявления корреляционной чвязи между двумя количественными показателями x и y удобнее пользоваться методом группировок. Чтобы выявить наличие корреляционной связи между x и y строят групповую или корреляционную таблицы. В первом случае проводится группировка по факторному признаку x и для каждой выделенной группы рассчитывается среднее значение результативного признака 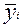. Если y зависит от x, то в изменении среднего значения будет прослеживаться определенная закономерность. Покажем это на том же примере, сгруппировав предприятия (табл. 2.1-1)

Из табл.2.1-1 видно, что средний выпуск по предприятиям (графа 4)

неуклонно растет от групп с небольшими основными фондами к

группам более крупных предприятий, что подтверждает

закономерность, чем больше фондов x , тем больше средний выпуск y.

Таблица 2.1-1

Показатели деятельности предприятий по группам

Основные производственные фонды, млн.руб.   xi	Количество предприятий	Валовый выпуск продукции, млн. руб.
fi	∑yi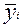
Менее 20
21-50			55,75
51-80
Свыше 80
Итого

Если в таблицах группировки осуществляются по двум признакам (количественным), то они называются корреляционными.В подлежащем такой таблицы выделяются группы по факторному признаку x, а в сказуемом - группы по результативному признаку (или наоборот), а в клетках таблицы на пересечении x и y показано число случаев совпадения каждого значения x c соответствующим значением y. Рассмотрим построение и использование корреляцинной таблицы 2.3 на примере [16, c. 207) зависимости производительности труда рабочих y (число изделий в час) от стажа работы x (лет). Число рабочих n= 40.

Таблица 2.3

Корреляционная таблица

Значение признака xi	Значение признака yi	Итого (число единиц) fx = fj	Среднее значение по груп-пам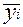
			-	-		8,75
				-		12,08
	-					15,31
	-	-				16,87
Итого (число единиц fy =fi					∑fj = 40	14,00

В первой строке значению признака x=1 один раз соответствует значение y=5 и три раза y =10. Аналогично во второй строке, где x = 3 , у = 5 соответствует 2 раза, y = 10 – 3 раза и т.д.. В итоговой строке показано распределение всех 40 единиц по признаку y, поэтому и частоты обозначены как f_y.

В итоговом столбце (графа 6) показано распределение тех же 40 единиц по признаку x ( обозначено fj). Каждая частота внутри таблицы- это f_xy. Для каждого j-го значения факторного признака x рассчитаем среднее значение результативного признака 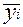(графа 7). Например, по первой строке 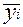= 8,75, по второй строке – 12,08 и т.д.. Это групповые средние результативного признака. Общая средняя рассчитывается по распределению итоговой строки:

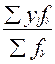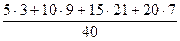= = 560/40 = 14.

Из таблицы 2.3. видно, что по мере увеличения значений x групповые средние значения 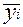увеличиваются от группы к группе, что позволяет сделать вывод о том, что между стажем работы x и производительностью труда y существует корреляционная связь.

О наличии и направлении связи можно судить и по «внешнему виду» таблицы, то есть по расположению в ней частот. Если частоты расположены в клетках беспорядочно, то это свидетельствует об отсутствии связи или незначительной зависимости y от x. Если частоты расположены по диагонали из верхнего левого угла в нижний правый угол, то это свидетельствует о прямой линейной зависимости между показателями x и y. Расположение по диагонали из нижнего левого угла в верхний правый свидетельствует об обратной линейной зависимости. В приведенном примере (табл.2.2) распределение частот по диагонали из верхнего левого угла в нижний правый угол, свидетельствует о прямой линейной зависимости между показателями стажа работы x и производительности труда y.

При построении эмпирической линии регрессии по данным корреляционной таблицы в качестве x принимаются значения середины интервалов факторного признака, а в качестве y – групповые средние результативного прзнака 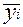. Если наличие корреляции выявляется графически, предпочтительнее по исходным данным строить «корреляционное поле», а затем на его фоне по средним значениям y – эмпирическую линию регрессии.

Коррекционное поле представляет, по сути, ту же корреляцинную таблицу, только в клетках вместо чисел (частот) проставлены соответствующие точки на плоскости пары x и y. Корреляционное поле не только отражает общую зависимость между x и y, но и концентрацию индивидуальных точек вокруг линии регрессии показателя .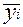

На основе аналитических групповых и корреляционных таблиц можно измерить тесноту связи с помощью эмпирического корреляционного отношения

, , ,

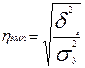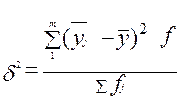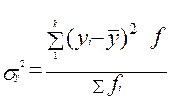где 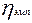– эмпирическое корреляционное отношение;

δ² –общая дисперсия;

σ_y² - межгрупповая дисперсия;

f_j = f_x – частота в j – ой группе x;

f_j = f_y - частота в i – ой группе y;

m – число групп по факторному признаку x;

k – число групп по результативному признаку y;

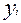– индивидуальные значения результативного признака;

– общее среднее значение результативного признака;

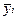- средние значения результативного признака по группам.

Квадрат эмпирического корреляционного отношения, то есть 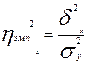, называется эмпирическим коэффициентом детерминации.

В нашем примере межгрупповая дисперсия равна:

= =

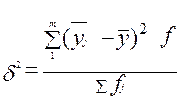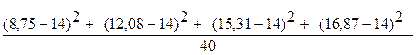[(-5,25)² +(-1, 92)² + (1,31)²+(2,87)²]/40= (27,5625+3,6864 + 1,7161+ 8,2369)/40 = 41,2019/40 =1,0300475;

Общая дисперсия равна:

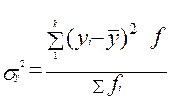= [3(5-14)²+ 9(10-14)²+ 21(15-14)² + 7(20-14)²]/40 =

[3(-9)²+ 9(-4)²+ 21(1)² + 7(6)²]/40= [3*81+ 9*16+ 21 + 7*36]/40=[3*81+ 9*16+ 21 + 7*36]/40 = (243 + 144 + 21 +252)/40 = 660/40 = 16,5;

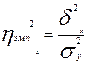= 1,03/16,5 = 0,062

Извлекая квадратный корень, получим:

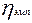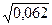= = 0.2598.

Полученное значение эмпирического корреляционного отношения 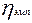= 0,26 характеризует тесноту связей, как очень слабую (<0,3), то есть производительность труда хотя и зависит от стажа работников, но значительно больше зависит от других факторов (фондовооруженности, квалификации и т.д.).