Нормальное распределение непрерывной случайной величины. Вычисление попадания в заданный интервал нормально распределенной случайной величины. Правило трёх сигм.

Закон распределения вероятностей непрерывной случайной величины Х называется нормальным распределением Гаусса, если её плотность вероятности определяется формулой

,

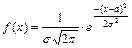(5.14)

где а и s называются параметрами распределения:

а =М(Х) – математическое ожидание,

s- среднеквадратическое отклонение случайной величины Х.

График плотности вероятности, который называется нормальной кривой, имеет вид (рис. 5.6):

Нормальное распределение с параметрами a=0, s=1 называется нормированным. Дифференциальная функция в случае такого распределения имеет вид:

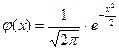
(5.15)

С этой функцией, а также с функцией 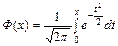и их свойствами мы уже встречались при рассмотрении локальной и интегральной теорем Лапласа. Их графики имеют вид (рис.5.7, рис.5.8):

Покажем влияние параметров а и s на вид кривой плотности вероятности. Как видно из графика (рис.5.9) параметр а определяет положение центра нормальной кривой и не влияет на форму кривой, s - разброс относительного центра (при уменьшении s растет f_max, а площадь должна остаться равной 1, кривая будет стягиваться к своей оси симметрии x=a, что соответствует смыслу s как меры рассеяния).

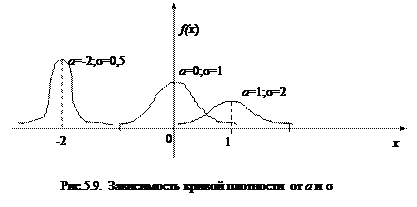Определим вероятность попадания нормально распределенной случайной величины Х в интервал (a;b):

.

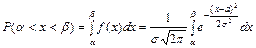Используя замену 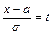, можно привести последний интеграл к виду

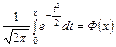, где Ф(х) функция Лапласа.

Таким образом, искомая вероятность может быть найдена по формуле

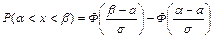
(5.16)

Отметим важный случай этой формулы, позволяющий оценить вероятность того, что случайная величина Х, распределенная по нормальному закону, отклонится от своего математического ожидания на величину, меньшую заданного положительного числа e, т.е. попадает в симметричный относительно математического ожидания интервал (а-e; a+e)

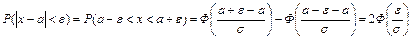
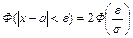
Используя данную формулу, можно получить известное правило “трех сигм”, которое утверждает, что нормально распределенная случайная величина практически не принимает значений вне интервала (а-3s;а+3s).

В самом деле:

,

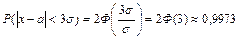а это означает, что событие, состоящее в том, что модуль отклонения нормально распределённой случайной величины от математического ожидания не превосходит утроенного среднего квадратического отклонения, имеет вероятность близкую к единице.