Проверка статистических гипотез

Условимся называть статистической гипотезой всякое предположение о виде закона распределения некоторого признака генеральной совокупности.

Проверку правильности или неправильности выдвинутой гипотезы проводят статистическими методами с помощью критерия согласия. Под критерием согласия подразумевают совокупность условий, подтверждающих справедливость принятой гипотезы. В результате такой проверки может быть принято правильное или неправильное решение. Поэтому при оценке согласованности выдвинутой гипотезы возможны ошибки двух типов: если отклоняется правильная гипотеза и если принимается ложная гипотеза.

Ошибки первого типа относятся к ошибкам первого рода; ошибки второго типа – к ошибкам второго рода.

Вероятность ошибки первого рода обычно обозначают через α и называют уровнем значимости критерия согласия.

Вероятность ошибки второго рода обозначают через β. Величину (1-β), т.е. вероятность того, что будет отвергнута ошибочная гипотеза, называют мощностью критерия.

Для проверки справедливости гипотезы о законе распределения случайной величины используют несколько критериев, различных по мощности и методу обработки исходных данных, из которых наиболее распространенными являются критерий Колмогорова и критерий χ² (хи-квадрат) Пирсона. Первый используется в случае, когда параметры распределения известны до опыта и требуется после опыта проверить согласованность теоретического и экспериментального распределения, второй – при неизвестных параметрах распределения.

Для применения критерия χ² при оценивании согласия теоретического и статистического распределений вариационный ряд эмпирических значений разбивают на k равных интервалов. Число значений ряда в интервале (эмпирическая частота) обозначают буквой n_i. Зная границы каждого интервала и принятый закон распределения, можно найти вероятность попадания случайной величины в этот интервал р_i. После этого из формулы 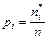находится теоретическая частота появления события 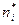. Для определения меры расхождения по критерию χ² используют выражение:

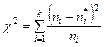
(9.1)

Полученное значение χ² сравнивают с критическим значением 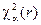этого критерия. Значение 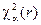выбирают по таблице в зависимости от уровня значимости α и числа степеней свободы r=k-1-m, где k – это число интервалов, m – число параметров предполагаемого распределения.

Гипотезу о предполагаемом законе распределения считают справедливой при условии 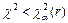. Если 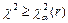, гипотезу отвергают.

Пример 9.1.По полученным в результате измерений данным (табл.9.1.) проверить гипотезу о нормальном распределении генеральной совокупности.

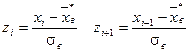
Таблица 9.1.

Номер интервала	Границы интервала	Частота	Середина интервала	Квадрат середины интервала	Разности	Границы
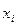
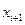
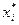
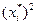
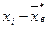
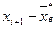
i			ni					zi	Zi+1
						-8,63	-6,63	-1,84	-1,41
						-6,63	-4,63	-1,41	-0,99
						-4,63	-2,63	-0,99	-0,56
						-2,63	-0,63	-0,56	-0,13
						-0,63	1,37	-0,13	0,29
						1,37	3,37	0,29	0,72
						3,37	5,37	0,72	1,14
						5,37	7,37	1,14	1,57
						7,37	9,37	1,57	1,99
Σ			n=200

Решение: Вычисляем среднее значение интервала 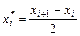и находим 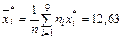.Далее находим 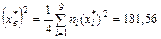. Используя для выборочной дисперсии формулу 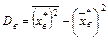, находим D_в=181,56-159,52=22,04. Отсюда .

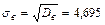Для того чтобы вычислить теоретические вероятности попадания случайных величин в интервалы (x_i, x_i+1), на основании таблиц функции Лапласа находим значения Ф(z_i) и Ф(z_i+1).

После этого составляем еще одну таблицу для расчета теоретических частот (табл.9.2)

Таблица 9.2

Номер интервала i	Границы	Ф(zi)	Ф(zi+1)	Pi= Ф(zi)- Ф(zi+1)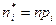
Zi	Zi+1
	-1,84	-1,41	-0,4671	-0,4207	0,0464	9,28
	-1,41	-0,99	-0,4207	-0,3389	0,0818	16,36
	-0,99	-0,56	-0,3389	-0,2123	0,1266	25,32
	-0,56	-0,13	-0,2123	-0,0517	0,1606	32,12
	-0,13	0,29	-0,0517	0,1141	0,1658	33,16
	0,29	0,72	0,1141	0,2642	0,1501	30,02
	0,72	1,14	0,2642	0,3729	0,1087	21,74
	1,14	1,57	0,3729	0,4418	0,0689	13,78
	1,57	1,99	0,4418	0,4767	0,0349	6,98

Составляем таблицу для определения 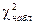(табл.9.3)

Таблица 9.3

i	ni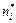
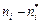
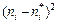
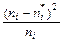
		9,28	5,72	32,7	3,52
		16,36	9,64	92,9	5,68
		25,32	-0,32	0,1
		32,12	-2,12	4,5	0,14
		33,16	-7,16	52,3	1,58
		30,02	-9,02	81,4	2,75
		21,74	2,26	5,1	0,23
		13,78	6,22	38,7	2,8
		6,98	6,02	36,2	5,2
å					21,9

Число степеней свободы r=9-3=6, по уровню значимости a=0,05 и r=6 из таблицы распределения c² находим 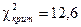. Так как 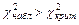, то гипотеза отвергается, следовательно, требуется либо изменить вид закона, либо повторить опыты.