Отыскание параметров выборочного уравнения линейной регрессии по несгруппированным данным

Так как по выборочным данным можно получить только оценки параметров, то оценку коэффициента а обозначим через r, а оценку b через b, т.е.

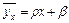
(11.1)

Обозначим через y_i значение величины y, соответствующее x_i, а через 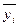- значение 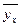, которое можно получить из выражения (12.1) при X=x_i,. Возьмем разности 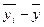, возведём их в квадрат и просуммируем. Получим функцию

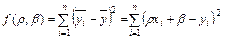
(11.2)

Определение параметров r и b в этом случае сводится к решению хорошо известной задачи нахождения минимума функции двух неизвестных.

Решив эту задачу, получим значения параметров r и b :

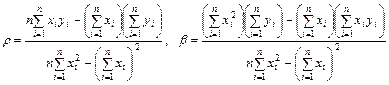
Аналогично находится выборочное уравнение линейной регрессии Х на У :

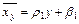, где

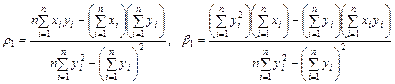
Для оценки связи между случайными величинами используется выборочный коэффициент корреляции. Для определения выборочного коэффициента корреляции сначала рассмотрим выборочный эмпирический корреляционный момент

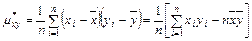
Выборочный коэффициент корреляции определяется по формуле

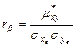
и обладает следующими свойствами:

1) ;

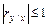2) Если 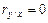, а линии регрессии прямые, то x и y не связаны между собой линейной корреляционной зависимостью;

3) Если 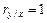, то x и y связаны линейной функциональной зависимостью.