Плотность распределения вероятностей. Определение, вероятностный смысл, свойства.
Кроме интегральной функции распределения для непрерывных случайных величин вводится понятие плотности распределения вероятностей или плотности вероятности.
Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x), равная производной интегральной функции
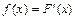
| (5.1) |
Из соотношения (5.1) можно найти функцию распределения, интегрируя плотность вероятности в общем случае от -¥ до рассматриваемого значения х, т.е.
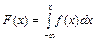
| (5.2) |
Плотность вероятности дает возможность найти вероятность того, что непрерывная случайная величина примет какое-нибудь значение из интервала (a,b).
Теорема.Вероятность того, что непрерывная случайная величина Х примет какое-нибудь значение из интервала (a,b), равна определенному интегралу от её плотности вероятности в пределах от a до b:
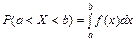
| (5.3) |
Смысл плотности распределения вероятности состоит в том, что она указывает на то, как часто появляется случайная величина Х в некоторой окрестности точки х при повторении опытов.
Свойства функции f(x):
1. f(x)³0, т.к. плотность распределения является производной от её интегральной функции распределения, а функция распределения - неубывающая функция.
2. 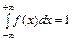 . В самом деле, по формуле (5.3)
. В самом деле, по формуле (5.3) 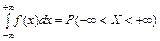 , а событие ‑¥<X<+¥ является достоверным событием, следовательно, его вероятность равна единице, т.е.
, а событие ‑¥<X<+¥ является достоверным событием, следовательно, его вероятность равна единице, т.е.
Р(‑¥<X<+¥ )=1, а это значит, что и 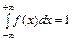 .
.
Пример 5.2.Плотность распределения непрерывной случайной величины Х задана на всей оси ОХ равенством 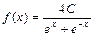 .
.
Найти постоянный параметр С.
Решение: Плотность распределения f(x) должна удовлетворять условию 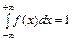 .
.
Потребуем, чтобы это условие выполнялось
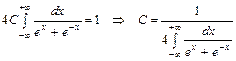
Вычислим несобственный интеграл:
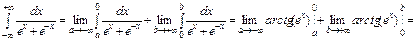
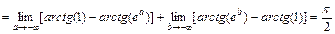
Таким образом,

Окончательно получим 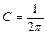 .
.
Дата добавления: 2020-10-25; просмотров: 567;











