Задачи теории корреляции

Функциональной зависимостью называется такая связь между переменными величинами, при которой зависимая величина - функция - полностью определяется значениями влияющих независимых величин - аргументов. Вид зависимости между аргументами и функцией обычно задается в виде формулы.

Наиболее часто на практике используются: линейная функция y=ax+b, гиперболическая 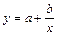, показательная - 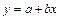, степенная (обычно парабола) - .

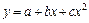Корреляционная зависимость - это такая связь между величинами, когда определенным значениям влияющих величин - факторов соответствуют множество значений зависимой величины, распределенных по известному закону распределения.

Например, чем больше товарооборот x, тем больше должна быть сумма издержек обращения y(x), однако, если фактические данные о товарообороте и издержках, полученных от разных потребительских обществ, нанести в виде точек на координатную плоскость (x,y), то они могут иметь вид прямолинейного вытянутого облака -корреляционного поля (рис.10.1.)

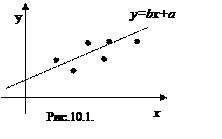Под корреляционной зависимостью y от x понимается зависимость условной средней 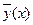от x, т.е. 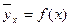. Это равенство называется уравнением регрессии y на х. Вместе с регрессией y на х всегда может быть построена и регрессия x на y, с уравнением .

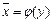При определении корреляционной зависимости, решаются две задачи:

1. установить форму корреляционной зависимости, т.е. вид функции;

2. оценить тесноту (силу) корреляционной связи (она оценивается по величине рассеяния значений y вокруг условного среднего 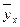. Чем меньше рассеяние, тем сильнее корреляционная зависимость).