Локальная теорема муавра-Лапласа
Если вероятность наступления события А в каждом из n независимых испытаниях постоянна, то вероятность появления этого события в n независимых испытаниях ровно m раз определяется формулой Бернулли. Если число испытаний велико, то вычисление искомой вероятности по формуле Бернулли становится очень громоздким. В этом случае для нахождения вероятности 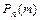 формулу Бернулли нецелесообразно использовать. В таких случаях используют формулу, которая определяется локальной теоремой Муавра-Лапласа.
формулу Бернулли нецелесообразно использовать. В таких случаях используют формулу, которая определяется локальной теоремой Муавра-Лапласа.
Теорема. Если вероятность р наступления события А в каждом испытании постоянна, отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность 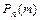 того, что в n независимых испытаниях событие А наступит m раз находится по формуле:
того, что в n независимых испытаниях событие А наступит m раз находится по формуле:
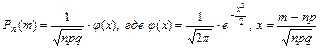
| (3.3) |
Функция j(x) табулирована. Учитывая, что функция j(x) четная, т.е. j(-x)= j(x), в таблице приведены значения j(x) только для положительных значений аргумента. При использовании формулы (3.3) нужно иметь ввиду, что если х>4, то j(x)»0.
Пример 3.4. Найти вероятность того, что событие А наступит 1400 раз в 2400 испытаниях, если вероятность появления этого события в каждом испытании равна 0,6.
Решение: Так как n велико, воспользуемся локальной теоремой Лапласа. Вычислим
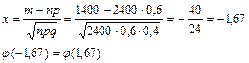
По таблице найдем j(1,67)=0,0989.
Искомая вероятность 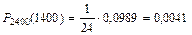 .
.
Дата добавления: 2020-10-25; просмотров: 480;











