Интегральная функция распределения: её свойства и график

В теории вероятностей часто приходится иметь дело с такими случайными величинами, возможные значения которых, сплошь заполняют некоторый конечный или бесконечный интервал. Например, электрическая лампочка испытывается на длительность горения. Случайная величина Х – полное время горения лампочки является непрерывной случайной величиной.

Составить таблицу, в которой были бы перечислены все возможные значения непрерывных случайных величин и указаны их вероятности, невозможно, так как таких значений бесконечное множество.

Для характеристики непрерывной случайной величины используется функция распределения вероятностей F(x), которая представляет собой вероятность события Х<х: 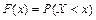. Ее называют интегральной функцией распределения. При любом х=х₀ значение F(x₀) задается равенством 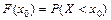. То есть для количественной характеристики распределения вероятностей удобно пользоваться не вероятностью того, что случайная величина Х примет некоторое данное значение х₀, а вероятностью того, что случайная величина примет значение, меньше х₀, т.е. .

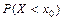Свойства интегральной функции распределения F(x):

1. Значение интегральной функции распределения принадлежит отрезку [0;1]: .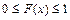

2.Интегральная функция распределения есть неубывающая функция .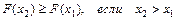

3. Вероятность того, что случайная величина Х примет значение, заключенное в интервале (a;b), равна приращению интегральной функции распределения на этом интервале

.

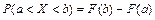4. Если все возможные значения случайной величины Х принадлежат интервалу (a;b), то

.

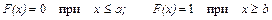5. Справедливы следующие предельные соотношения

.

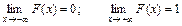Пример 5.1.Дискретная случайная величина Х задана законом распределения

Найти функцию распределения F(x), изобразить её график.

Решение: Если x£2, то F(x)=0. Действительно, значений меньших числа 2, величина Х не принимает. Следовательно, при х£2 функция F(x)=P(X<x)=0.

Если 2<х£4, то F(x)=0.5. Действительно, Х может принимать значение 2 с вероятностью 0,5.

Если 4<х£7, то F(x)=0.7. Действительно, Х может принимать значение 2 с вероятностью 0,5 и значение 4 с вероятностью 0,2. Следовательно, одно из этих значений, безразлично какое, Х может принять с вероятностью 0,5+0,2=0,7 .

Если х>7, то F(x)=1.

Итак, искомая функция распределения имеет вид:

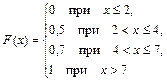
График этой функции приведен на рис.5.1