Теорема сложения вероятностей для НЕсовместных и совместных событий. Вероятность появления хотя бы одного события. Теоремы умножения для двух независимых и зависимых событий
 |
Суммой А+В двух событий А и В называется событие, состоящее в появлении либо события А, либо события В, либо обоих этих событий вместе (рис.2.1).
Теорема. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий:
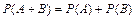
| (2.4) |
Теорема. Вероятность суммы нескольких попарно несовместных событий равна сумме вероятностей этих событий:
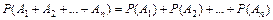
| (2.5) |
Следствие 1. Если события А1, А2, … Аn образуют полную группу событий, то сумма их вероятностей равна 1:
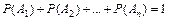
| (2.6) |
Пример 2.5. В лотерее 1000 билетов, из них на один билет выпадает выигрыш 5000 рублей, на 10 билетов – выигрыш по 1000 рублей, на 50 билетов – выигрыши по 200 рублей, на 100 билетов – выигрыши по 50 рублей, остальные билеты невыигрышные. Некто покупает один билет. Найти вероятность выигрыша не менее 200 рублей.
Решение:Рассмотрим события:
А – выиграть не менее 200 руб.,
А1 – выиграть 200 руб.,
А2 – выиграть 1000 руб.,
А3 – выиграть 5000 руб.
Очевидно, что
А=А1+А2+А3
По теореме сложения вероятностей несовместных событий
Р(А)=Р(А1)+Р(А2)+Р(А3)=0,05+0,01+0,001=0,061.
Теорема. Вероятность суммы двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:
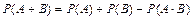
| (2.7) |
Произведением двух событий А и В называется событие, состоящее в появлении и события А, и события В (рис.2.2).
Пусть события А и В – зависимые события. Условной вероятностью РА(B) события В называется вероятность события В, найденная в предположении, что событие А уже наступило.
Событие В называют независимым от события А, если появление события А не изменяет вероятности события В.
 |
Теорема. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:
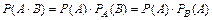
| (2.8) |
В частности, для независимых событий:
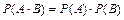
| (2.9) |
т.е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.
Пример 2.6. Игральный кубик подбрасывают 2 раза. Какова вероятность того, что оба раза выпадет «шестерка»?
Решение: Рассмотрим события: А – первый раз выпадет «шестерка» 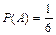 и В – второй раз выпадет «шестерка»
и В – второй раз выпадет «шестерка» 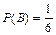 . События А и В независимы. Тогда
. События А и В независимы. Тогда 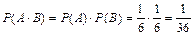
Пример 2.7. В цехе работают семь мужчин и три женщины. По табельным номерам наудачу отобраны три человека. Найти вероятность того, что все отобранные лица окажутся мужчинами.
Решение: Введем обозначение событий. А – первым отобран мужчина, В – вторым отобран мужчина, С – третьим отобран мужчина.
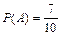
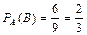
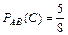
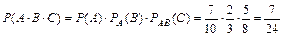
Теорема.Вероятность появления хотя бы одного из событий А1, А2,…, Аn, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий :
:
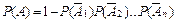
| (2.10) |
Пример 2.8. Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель первым стрелком равна 0,7; вторым – 0,8; третьим – 0,9. Найти вероятность того, что: a) все три стрелка попадут в цель; b) все три стрелка промахнутся; c) только один попадет; d) только два стрелка попадут в цель; e) не более двух стрелков попадут; f) хотя бы один стрелок попадет в цель.
Решение:
a) Пусть событие А – все три стрелка попадут в мишень. Обозначим вероятность того, что первый стрелок попадет в цель Р(1)=0,7; второй – Р(2)=0,8; третий – Р(3)=0,9.
Тогда 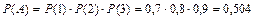 .
.
b) Обозначим вероятность того, что промахнется первый стрелок - 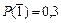 ; промахнется второй –
; промахнется второй – 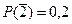 ; промахнется третий –
; промахнется третий – 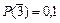 .
.
Событие В – все три стрелка промахнулись.
Тогда 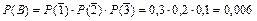 .
.
c) Пусть событие С состоит в том, что только один стрелок попадет в цель. Событие С произойдет, если произойдет либо событие А1: 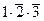 , либо событие А2:
, либо событие А2: 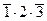 , либо событие А3:
, либо событие А3: 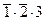 . Переходя к вероятностям, получим:
. Переходя к вероятностям, получим:
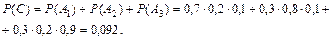
d) Рассуждая аналогично предыдущему случаю, получим:
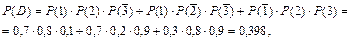
где D – событие, состоящее в том, что только два стрелка попадут в цель.
e) Не более двух стрелков попадут в мишень, если произойдет либо событие B – все три стрелка промахнутся, либо событие С – только один стрелок попадет в мишень, либо событие D – только два стрелка попадут в мишень. Вероятности событий B, С, D известны: Р(B)=0,006, Р(С)=0,092, Р(D)=0,398. Следовательно,
Р(E) = Р(В) + Р(С) + Р(Д) = 0,496, где E – событие, состоящее в том, что в результате опыта не более двух стрелков попадут в цель.
f) Рассмотрим два события: F – хотя бы один стрелок попадет в мишень; событие B- все трое промахнутся. Эти события являются противоположными, следовательно:
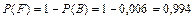 .
.
Дата добавления: 2020-10-25; просмотров: 553;











