Числовые характеристики дискретной случайной величины
Закон распределения полностью характеризует случайную величину. Зная закон распределения случайной величины, можно указать интервал расположения возможных значений случайной величины и какова вероятность её появления в том или ином интервале. Однако встречаются случаи, когда закон распределения случайной величины неизвестен. В таких случаях случайную величину изучают по её числовым характеристикам. Такими характеристиками являются математическое ожидание, дисперсия и среднее квадратическое отклонение.
Математическим ожиданием М(Х) дискретной случайной величины Х называется сумма произведений всех её значений на соответствующие им вероятности.
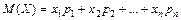
| (4.1) |
Смысл М(Х) в том, что около него колеблется среднее арифметическое значений, принимаемых случайной величиной Х в большой серии опытов. Математическое ожидание М(Х) называют также средним значением случайной величины Х, подчеркивая тем самым статистический смысл этой величины.
Свойства математического ожидания:
1. Математическое ожидание постоянной величины равно самой постоянной, т.е. М(С)=С.
2. Постоянный множитель можно выносить за знак М(Х)
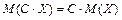 .
.
3. Математическое ожидание алгебраической суммы двух (или нескольких) случайных величин равно алгебраической сумме их математических ожиданий, т.е.
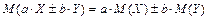 .
.
4. Для независимых случайных величин Х и Y (две случайные величины называются независимыми, если закон распределения одной случайной величины не зависит от того, какие возможные значения принимает другая величина)
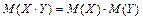 .
.
В большинстве случаев только математическое ожидание не может в достаточной степени характеризовать случайную величину.
Пусть две случайные величины X и Y заданы своими законами распределения:
| X | -1 | Y | -100 | |||
| p | 1/2 | 1/2 | p | 1/2 | 1/2 |
Математические ожидания величин Х и Y одинаковы - М(X)=М(Y)=0. Однако характер распределения их различный: возможные значения величины Х расположены гораздо ближе к своему математическому ожиданию, чем значения величины Y, т.е. величина Y сильнее отклоняется от своего математического ожидания, чем величина Х.
Рассмотрим еще одну числовую характеристику, показывающую степень рассеяния значений случайной величины относительно центра (т.е. М(X)). Эта характеристика называется дисперсиейслучайной величины Х и определяется по формуле
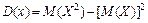
| (4.2) |
Содержательный смысл дисперсии – мера рассеяния значений случайной величины вокруг её математического ожидания.
Свойства дисперсии:
1. Дисперсия постоянной величины равна нулю, т.е. D(C)=0.
2. Постоянный множитель можно выносить за знак дисперсии, возведя в квадрат, т.е. 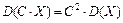 .
.
3. Для независимых случайных величин Х и Y дисперсия их алгебраической суммы равна сумме дисперсий, т.е. 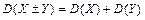 .
.
Из определения дисперсии можно получить более удобную формулу для её вычисления:
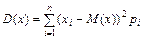 или
или
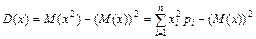
| (4.3) |
Дисперсия случайной величины измеряется в квадратных единицах относительно размерности самой случайной величины. В тех случаях, когда нужно иметь числовую характеристику рассеяния возможных значений в той же размерности, что и сама случайная величина, используется среднее квадратическое отклонение.
Средним квадратическим отклонением s(X) случайной величины Х называется корень квадратный из её дисперсии:
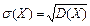 . .
| (4.4) |
Пример 4.1.Случайная величина Х – число очков, выпавших при однократном бросании игральной кости. Определить s(X).
Решение:
| х | ||||||
| p | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 | 1/6 |
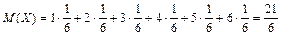
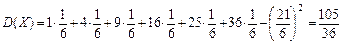
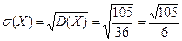 .
.
Дата добавления: 2020-10-25; просмотров: 536;











