Формула полной вероятности
Теорема. Если события Н1, Н2,… Нn образуют полную группу несовместных событий и событие А может наступить лишь при условии появления одного из событий Нi (i=1,2,…,n), то имеет место формула, которая называется формулой полной вероятности:
| Р(А) =Р(Н1) Р(А/ Н1)+…+ Р(Нn) Р(А/ Нn) | (2.11) |
Входящие в формулу события Н1, Н2,… Нn называют гипотезами.
Пример 2.9. В урну, содержащую два шара, опущен белый шар, после чего из неё наудачу извлечен один шар. Найти вероятность того, что извлеченный шар окажется белым, если одинаково возможны все предположения о первоначальном составе шаров (по цвету).
Решение: Обозначим через А событие - извлечен белый шар. Возможны следующие предположения (гипотезы) о первоначальном составе шаров:
В1 - белых шаров нет, В2 - один белый шар, В3 - два белых шара.
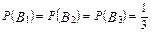 |
Поскольку всего имеется три гипотезы, причем по условию они равновероятны,
и сумма вероятностей гипотез равна единице, то условная вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне не было белых шаров, 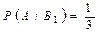
Условная вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне был один белый шар, 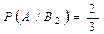 .
.
Условная вероятность того, что будет извлечен белый шар, при условии, что первоначально в урне было 2 белых шара, 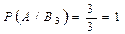 .
.
Искомую вероятность того, что будет извлечен белый шар, находим по формуле полной вероятности:
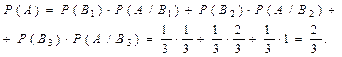 .
.
Формула Байеса
Теорема.Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) Н1, Н2,… Нn, которые образуют полную группу событий. Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формуле Байеса
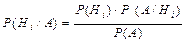 , (i=1,2,…n),
где Р(А) =Р(Н1) Р(А/ Н1)+…+ Р(Нn) Р(А/ Нn). , (i=1,2,…n),
где Р(А) =Р(Н1) Р(А/ Н1)+…+ Р(Нn) Р(А/ Нn).
| (2.12) |
Пример 2.10.В группе из 10 студентов, пришедших на экзамен, 3 подготовлены отлично, 4 – хорошо, 2 – удовлетворительно и 1 – плохо. Имеется 20 вопросов, причем: отлично подготовленный студент может ответить на все вопросы, хорошо подготовленный – на 16, удовлетворительно подготовленный – на 10 и плохо подготовленный – на 5. Найти вероятность того, что случайно выбранный студент сможет ответить на доставшийся ему вопрос, и вероятность того, что этот студент плохо подготовлен и ему просто повезло с вопросом.
Решение:Введем следующие обозначения для заданных величин:
Н1 – студент отличник
Н2 – студент учится хорошо
Н3 - студент учится удовлетворительно
Н4 – студент учится плохо
А – вопрос “хороший”
P(H1)=0,3 (3 из 10)
P(Н2)=0,4 (4 из 10)
P(Н3)=0,2 (2 из 10)
P(Н4)=0,1 (1 из 10)
P(A/H1)=20/20=1
P(А/Н2)= 16/20=0,8
P(А/Н3)=10/20=0,5
P(А/Н4)=5/20=0,25
Воспользуемся формулой полной вероятности для вычисления P(А): 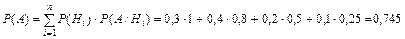
и формулой Байеса для вычисления P(Н4/А):
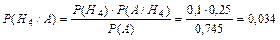 .
.
Дата добавления: 2020-10-25; просмотров: 489;











