Повторение независимых испытаний
Пусть в общем случае проводится n независимых испытаний. Поставим задачу: определить вероятность того, что в n испытаниях ровно m раз наступит событие А, если вероятность его наступления в каждом испытании равна p. Эта вероятность обозначается символом Рn(m) и определяется по формуле:
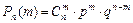 , ,
| (3.1) |
где q=1-p
Формула (3.1) называется формулой Бернулли.
Пример 3.1.Два равносильных шахматиста играют в шахматы. Что вероятнее: выиграть две партии из четырех или три партии из шести (ничьи во внимание не принимаются).
Решении:. Играют равносильные шахматисты, поэтому вероятность выигрыша 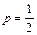 . Следовательно, вероятность проигрыша
. Следовательно, вероятность проигрыша 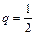 . Так как во всех партиях вероятность выигрыша постоянна, то применима формула Бернулли.
. Так как во всех партиях вероятность выигрыша постоянна, то применима формула Бернулли.
Найдем вероятность того, что две партии из четырех будут выиграны:
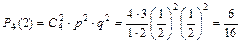
|
Найдем вероятность того, что будут выиграны три партии из шести:
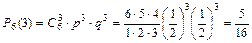
|
Так как 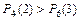 , то вероятнее выиграть две партии из четырех, чем три партии из шести.
, то вероятнее выиграть две партии из четырех, чем три партии из шести.
Наивероятнейшим числом 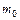 появления события А в n независимых испытаниях называется число, для которого вероятность
появления события А в n независимых испытаниях называется число, для которого вероятность 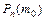 превышает или, по крайней мере, не меньше вероятности каждого из остальных возможных исходов испытания. Это число определяется из неравенства:
превышает или, по крайней мере, не меньше вероятности каждого из остальных возможных исходов испытания. Это число определяется из неравенства: 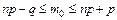 . Если числа np-q и np+p – дробные, то число m0 –единственное. Если же числа np-q и np+p – целые, то будет два значения наивероятнейшего числа m0.
. Если числа np-q и np+p – дробные, то число m0 –единственное. Если же числа np-q и np+p – целые, то будет два значения наивероятнейшего числа m0.
Пример 3.2.Три раза подбрасывают монету. Найти наивероятнейшее число появлений герба.
Решение: 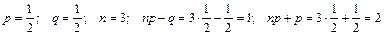
Откуда 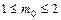 . Следовательно, вероятнее всего, герб появится либо один раз, либо два раза.
. Следовательно, вероятнее всего, герб появится либо один раз, либо два раза.
Формула Пуассона
Формула Бернулли удобна для вычислений при сравнительно небольшом числе испытаний n. При больших значениях n и малом значении вероятности p (например, n>100 и λ=np<10) хорошее приближение для формулы Бернулли дает формула Пуассона.
Теорема.Если вероятность р наступления события А в каждом испытании постоянна и мала, а число независимых испытаний n достаточно велико, то вероятность того, что событие А наступит m раз приближенно равна: 
 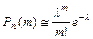 , ,
| (3.2) |
где l=np.
Пример 3.3.Завод отправил потребителю 500 изделий. Вероятность повреждения изделия в пути равна 0,002. Найти вероятность того, что в пути будет повреждено три изделия.
Решении:. Число n=500 велико, вероятность р=0,002 мала, а произведение l=np=1. Следовательно, применима формула Пуассона 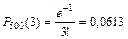 .
.
Дата добавления: 2020-10-25; просмотров: 628;











