Основные формулы комбинаторики
Основные теоремы теории вероятностей
Часто при вычислении вероятности события с использованием формулы (1.1) применяют формулы комбинаторики, по которым находят число благоприятствующих исходов и общее число возможных исходов.
Основные формулы комбинаторики
Комбинаторика – раздел математики, изучающий вопросы о том, сколько комбинаций определенного типа можно составить из данных предметов (элементов).
Как при решении задач с использованием классического определения вероятности, так и в дальнейшем нам понадобятся некоторые формулы комбинаторики. Приведем наиболее употребительные из них.
Размещениями из n различных элементов по m элементов (m≤n) 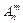 называются упорядоченные выборки, объемом m элементов, отобранные из n элементов, которые отличаются либо самими элементами, либо порядком расположения элементов.
называются упорядоченные выборки, объемом m элементов, отобранные из n элементов, которые отличаются либо самими элементами, либо порядком расположения элементов.
Например, из трех элементов a, b, c можно составить по два элемента следующие размещения: ab, ac, bc, ba, ca, cb
Число размещений из n элементов по m элементов определяется по формуле:
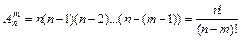
| (2.1) |
Пример 2.1. В высшей лиге чемпионата по футболу 16 команд. Борьба идет за золотые, серебряные и бронзовые медали. Сколькими способами медали могут быть распределены между командами?
Решение: 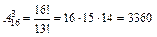 способами
способами
Если размещения из n элементов взяты по n (т.е. отличаются только порядком расположения элементов), то такие размещения называются перестановками- Рn.
Перестановки можно считать частным случаем размещений при m=n. Следовательно, число всех перестановок из n элементов вычисляется по формуле:
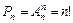
| (2.2) |
Пример 2.2.Сколько трехзначных чисел можно составить из цифр 1, 2, 3, если каждая цифра входит в изображение числа только один раз.
Решение: Искомое число трехзначных чисел Р3=3!=6.
Сочетаниями из n различных элементов по m элементов 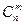 называются неупорядоченные выборки объемом m элементов из n элементов, которые отличаются хотя бы одним элементом.
называются неупорядоченные выборки объемом m элементов из n элементов, которые отличаются хотя бы одним элементом.
Другими словами, если из всех размещений, которые можно составить из n элементов по m, отберем только те, которые одно от другого отличаются хотя бы одним элементом, то получим число сочетаний из n элементов по m элементов.
Число сочетаний из n элементов по m элементов вычисляется по формуле:
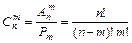
| (2.3) |
Отметим особенность формулы (2.3): 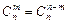 . Этим свойством удобно пользоваться, когда m>n/2.
. Этим свойством удобно пользоваться, когда m>n/2.
Пример 2.3. На тренировках занимаются 12 баскетболистов. Сколько может быть организовано разных стартовых пятерок?
Решение: 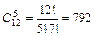 .
.
Пример 2.4. В партии из N деталей имеется n стандартных. Наудачу отобраны m деталей. Найти вероятность того, что среди отобранных деталей ровно k стандартных.
Решение: Общее число возможных элементарных исходов испытания равно числу способов, которыми можно извлечь m деталей из N деталей, т.е.  . Подсчитаем число исходов, благоприятствующих интересующему нас событию (среди m деталей ровно k стандартных): k стандартных деталей можно взять из n стандартных деталей
. Подсчитаем число исходов, благоприятствующих интересующему нас событию (среди m деталей ровно k стандартных): k стандартных деталей можно взять из n стандартных деталей 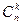 способами; при этом остальные m-k деталей должны быть нестандартными; взять же m-k нестандартных деталей из N-n нестандартных можно
способами; при этом остальные m-k деталей должны быть нестандартными; взять же m-k нестандартных деталей из N-n нестандартных можно 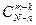 способами. Следовательно, число благоприятствующих исходов равно
способами. Следовательно, число благоприятствующих исходов равно 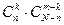 .
.
Тогда вероятность того, что среди отобранных деталей ровно k стандартных равна: 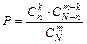 .
.
.
Дата добавления: 2020-10-25; просмотров: 449;











