Смежные классы, теорема Лагранжа

Пусть H подгруппа группы G. Левым смежным классом элемента a по подгруппе H называется множество элементов ah, где h принадлежит H. Левый смежный класс обозначают aH. Аналогично вводится правый смежный класс элемента a по подгруппе H, который обозначают Ha.

Поскольку в подгруппе всегда имеется нейтральный элемент, то каждый элемент a содержится в смежном классе aH (Ha).

Свойство 2.7. Элементы a и b принадлежат одному левому смежному классу по подгруппе H тогда и только тогда, когда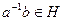

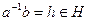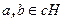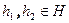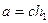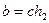Доказательство. Если , то b=ah, и, значит, b принадлежит левому смежному классу aH. Обратно, пусть , тогда найдутся , что , и .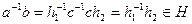

Теорема 2.2. Если левые (правые) смежные классы элементов a и b по подгруппе H имеют общий элемент, то они совпадают.

Доказательство. Пусть 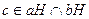. Тогда найдутся 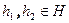, что 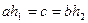. Произвольный элемент из левого смежного класса aH содержится в левом смежном классе bH. Действительно, 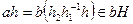для 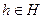, и, следовательно, 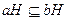. Аналогично доказывается включение 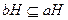. Тем самым теорема доказана.

Следствие 2.1. Левые смежные классы либо не пересекаются, либо совпадают.

Доказательство очевидно.

Следствие 2.2. Левый (правый) смежный класс равномощен H.

Доказательство. Установим соответствие межу элементами подгруппы H и элементами смежного класса aH по формуле 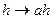. Соответствие является взаимно однозначным. Тем самым утверждение доказано.

Теорема 2.3 (Лагранжа). Порядок конечной группы делится на порядок ее подгруппы.

Доказательство. Пусть G – группа порядка n, а H - подгруппа G порядка k.Имеет место равенство 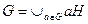. Удалим из правой части равенства повторяющиеся члены. В результате останутся не пересекающиеся смежные классы. Поскольку число элементов в смежном классе равн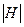о , то 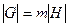, где m количество различных смежных классов. Тем самым установлено равенство n=mk, что и требовалось.

Количество различных смежных классов называется индексом подгруппы H в группе G.