Интегральная теорема Лапласа
Предположим, что производится п испытаний, в каждом из которых вероятность появления события А постоянна и равна р (0 < р < 1). Как вычислить вероятность 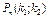 того, что событие А появится в п испытаниях не менее
того, что событие А появится в п испытаниях не менее 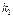 и не более
и не более 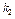 раз?
раз?
На этот вопрос отвечает интегральная теорема Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 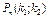 того, что событие А появится в п испытаниях от
того, что событие А появится в п испытаниях от 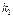 до
до 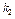 раз, приближенно равна определенному интегралу:
раз, приближенно равна определенному интегралу:

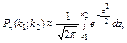
где 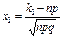 и
и 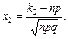
При решении задач, требующих применения интегральной теоремы Лапласа, пользуются специальными таблицами (Приложение 2), так как неопределенный интеграл не  не выражается через элементарные функции. В таблице даны значения функции Ф(х) для положительных значений х и для х = 0; для х < 0 пользуются той же таблицей (функция Ф(х) нечетна, т. е. Ф(–х) = – Ф(х)) В таблице приведены значения интеграла лишь до х = 5, так как для х > 5 можно принять Ф (х) = 0,5.
не выражается через элементарные функции. В таблице даны значения функции Ф(х) для положительных значений х и для х = 0; для х < 0 пользуются той же таблицей (функция Ф(х) нечетна, т. е. Ф(–х) = – Ф(х)) В таблице приведены значения интеграла лишь до х = 5, так как для х > 5 можно принять Ф (х) = 0,5.
Функцию Ф(х) часто называют функцией Лапласа.
Для того чтобы можно было пользоваться таблицей функции Лапласа, выполним следующие преобразования:
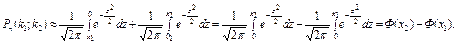
Итак, вероятность того, что событие А появится в п независимых испытаниях от 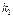 до
до 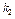 раз,
раз,
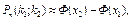
где 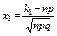 и
и 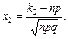
Пример 3.5. Вероятность того, что деталь не прошла проверку ОТК, равна р = 0,2. Найти вероятность того, что среди 400 случайно отобранных деталей окажется непроверенных от 70 до 100 деталей.
Решение.
По условию, р = 0,2; q = 1 – p = 0,8; n = 400; 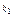 = 70;
= 70; 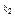 =100.
=100.
Воспользуемся интегральной теоремой Лапласа:
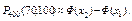
Вычислим нижний и верхний пределы интегрирования:
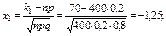
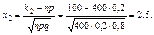
Таким образом, имеем
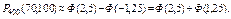
По таблице находим:

Искомая вероятность равна:
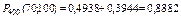
Литература:
1. Гмурман, В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В. Е. Гмурман. — 9-е изд., стер. — М.: Высш. шк., 2003. — с.55 – 61.
2. Гусак А.А. Теория вероятностей: справ. Пособие к решению задач / А.А. Гусак, Е.А. Бричикова. – 6-е изд. – Минск: ТетраСистемс, 2007. – с.173 – 184.
Контрольные вопросы:
1. Какой вид имеет формула Бернулли?
2. Каким должны быть события, чтобы можно было применить формулу Бернулли?
3. Как вычислить вероятность того, что в nнезависимых испытаниях событие наступит: а) менее k раз; б) более k раз; в) от k1 раз до k2 раз?
Дата добавления: 2016-07-27; просмотров: 2862;











