Циклические группы.

Множество элементов из группы G называется порождающим, если G получается замыканием этого множества относительно групповой операции.

Группа, порожденная одним элементом, называется циклической.

Следствие 2.3. Любая группа содержит циклическую подгруппу.

Доказательство. Пусть a –элемент группы G. Множество 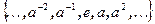является циклической подгруппой.

Порядок циклической подгруппы, порожденной элементом a, называется порядком элемента.

Свойство 2.8. Если элемент a имеет порядок n, то aⁿ=e.

Доказательство. Рассмотрим последовательность 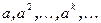. Поскольку число членов в последовательности бесконечно, а для степеней элемента a существует конечное число возможностей, то в последовательности встретятся одинаковые члены. Пусть 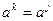, где k<j и k первый повторяющийся член. Тогда 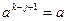, и значит, член k-j+1 повторяется. Следовательно, j=1 (иначе 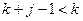). Таким образом, последовательность состоит из повторяющихся наборов вида 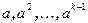и в ней k-1 различных элементов. Следовательно, k=n+1. Так как 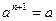, то .

Порядок любого элемента является делителем порядка группы, следовательно, a^|G|=e для любого элемента группы.

Следствие 2.4. Порядок группы делится без остатка на порядок любого элемента группы.

Доказательство очевидно.

Теорема 2.4 (о циклических группах)

I. Для любого натурального n существует циклическая группа порядка n.

II. Циклические группы одинаковых порядков изоморфны между собой.

III. Циклическая группа бесконечного порядка изоморфна группе целых чисел.

IV. Любая подгруппа циклической группы циклическая.

V. Для каждого делителя m числа n (и только для них) в циклической группе n-го порядка существует единственная подгруппа порядка m.

Доказательство. Множество комплексных корней степени n из 1 относительно операции умножения образует циклическую группу порядка n. Тем самым первое утверждение доказано.

Пусть циклическая группа G порядка n порождена элементом a, а циклическая группа H, того же порядка, порождена элементом b. Соответствие 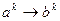взаимно однозначное и сохраняет операцию. Второе утверждение доказано

Циклическая группа бесконечного порядка, порожденная элементом a, состоит из элементов 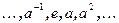. Соответствие 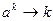является взаимно однозначным и сохраняет операцию. Таким образом, третье утверждение доказано.

Пусть H – подгруппа циклической группы G, порожденной элементом a. Элементы H являются степенью a. Выберем в H элемент, который является наименьшей по абсолютной величине ненулевой степенью a. Пусть это элемент 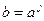. Покажем, что этот элемент является порождающим в подгруппе H. Возьмем произвольный элемент 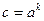из H. Произведение 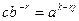содержится в H при любом r. Выберем r равным частному от деления k на j, тогда k-rj есть остаток от деления k на j и, значит, меньше j. Поскольку в H нет элементов, которые являются не нулевой степенью a, меньше чем j, то k-rj=0, и 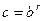. Четвертое утверждение доказано.

Пусть циклическая группа G порядка n порождена элементом a. Подгруппа, порожденная элементом 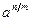, имеет порядок m. Рассмотрим подгруппу H порядка m. Выберем в H элемент, который является наименьшей по абсолютной величине ненулевой степенью a. Пусть это элемент 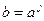. Покажем, что j=n/m. Элемент 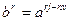принадлежит H. Следовательно, отличное от нуля число вида rj-nv по абсолютной величине не меньше j, что возможно только если n делится на j без остатка. Подгруппа, порожденная 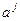, имеет порядок n/j=m, следовательно, j=n/m. Поскольку порождающий элемент подгруппы определяется однозначно по ее порядку, то пятое утверждение доказано.