Отношение, операция, алгебра.
Пусть M некоторое множество. Любое подмножество 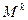 задает k-местное отношение (при k=1 отношение называется унарным, k=2 – бинарным), которое принимает значение «истина», если набор из k-элементов принадлежит
задает k-местное отношение (при k=1 отношение называется унарным, k=2 – бинарным), которое принимает значение «истина», если набор из k-элементов принадлежит 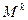 и «ложно» - иначе. Каждое k+1-местное отношение
и «ложно» - иначе. Каждое k+1-местное отношение 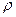 задает k-местную операцию (функцию) f следующим образом: набор
задает k-местную операцию (функцию) f следующим образом: набор 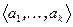 принадлежит
принадлежит 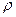 тогда и только тогда, когда
тогда и только тогда, когда 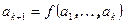 . При k=1 операция называется унарной, а при k=2 – бинарной. Бинарные операции часто записывают не в виде f(a,b) а как afb.
. При k=1 операция называется унарной, а при k=2 – бинарной. Бинарные операции часто записывают не в виде f(a,b) а как afb.
Множество M с определенными на нем отношениями и операциями называется алгеброй. Множество отношений и операций называется сигнатурой алгебры 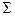 . Алгебру записывают как
. Алгебру записывают как 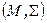 .
.
Допустим в множестве M нашлось такое подмножество U, что на нем определены все отношения и операции из 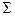 сигнатуры алгебры. Тогда алгебра
сигнатуры алгебры. Тогда алгебра 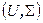 называется подалгеброй алгебры
называется подалгеброй алгебры 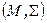 .
.
Полугруппа
Алгебра с одной бинарной ассоциативной операцией называется полугруппой. Бинарная операция называется ассоциативной, если (a*b)*c=a*(b*c). Часто, операцию в полугруппе называют произведением. В дальнейшем мы тоже будем придерживаться данного соглашения. Однако, следует помнить, что произведение в полугруппе не всегда коммутативная операция. Например, множество квадратных матриц порядка n с рациональными элементами относительно операции умножения матриц образуют полугруппу, и операция не коммутативна.
Свойство 2.1. Результат перемножения n элементов в полугруппе не зависит от способа расстановки скобок.
Доказательство проведем индукцией по числу сомножителей. При трех сомножителях утверждение очевидно. Пусть оно верно для любого числа сомножителей меньше n. Покажем его справедливость для n сомножителей. Выделим в произведении два элемента, умножаемых в последнюю очередь. Допустим 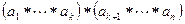 .Рассмотрим два случая.
.Рассмотрим два случая.
1. Пусть k=1. По предположению индукции в произведении 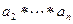 скобки можно расставлять произвольным образом. Расставим их следующим способом
скобки можно расставлять произвольным образом. Расставим их следующим способом 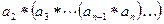 . В результате все произведение представится в виде
. В результате все произведение представится в виде 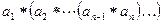 .
.
2. Пусть k=2,…,n-1. По предположению индукции в произведении 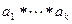 скобки можно расставлять произвольным образом. Расставим их следующим способом
скобки можно расставлять произвольным образом. Расставим их следующим способом 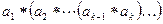 . В результате все произведение представится в виде
. В результате все произведение представится в виде 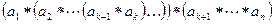 равное в силу ассоциативности операции
равное в силу ассоциативности операции 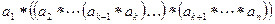 . Последнее произведение рассмотрено в случае 1.
. Последнее произведение рассмотрено в случае 1.
Таким образом, вне зависимости от расстановок скобок, результат равен 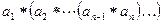 , что и доказывает требуемое утверждение.
, что и доказывает требуемое утверждение.
Элемент полугруппы 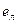 называется левым нейтральным (или левой единицей), если для любого другого элемента полугруппы a справедливо равенство
называется левым нейтральным (или левой единицей), если для любого другого элемента полугруппы a справедливо равенство 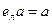 .
.
Аналогично вводится понятие правой единицы 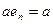 .
.
В полугруппе может существовать несколько левых (правых) единиц. Например, на множестве матриц вида 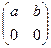 любая матрица вида
любая матрица вида 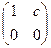 является левой единицей. Правых единиц нет.
является левой единицей. Правых единиц нет.
Свойство 2.2. Если в полугруппе есть левая и правая единица, то они равны.
Действительно, произведение 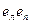 по определению левой единицы равно правой единице, а по определению правой единицы равно левой единице. Следовательно, левая и правая единицы равны.
по определению левой единицы равно правой единице, а по определению правой единицы равно левой единице. Следовательно, левая и правая единицы равны.
Полугруппа, в которой имеется левая и правая единица (которые в этом случае совпадают) называется полугруппой с единицей. Нейтральный элемент в этом случае обозначают через e (без индексов).
В полугруппе с единицей могут существовать решения уравнений ax=e и xa=e. Решение первого уравнения обозначается 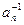 и называется правым обратным элементом к a, а решение второго уравнения обозначается
и называется правым обратным элементом к a, а решение второго уравнения обозначается 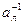 и называется левым обратным элементом к a.
и называется левым обратным элементом к a.
Свойство 2.3. Если к элементу полугруппы a существуют левый и правый обратные элементы, то они равны.
Доказательство вытекает из равенства 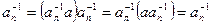 .
.
Если к элементу a существуют левый и правый обратные элементы, которые в этом случае совпадают, то тогда говорят об обратном элементе и обозначают его 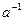 (без индексов).
(без индексов).
Группа, подгруппа
Полугруппа с единицей, для каждого элемента которой существует обратный элемент, называется группой. Другими словами, алгебра с одной бинарной операцией называется группой, если
1) Операция ассоциативна, т.е. (a*b)*c=a*(b*c)
2) Существует нейтральный элемент e ae=ea=a
3) Для каждого элемента группы a существует обратный элемент a-1, что a-1a =aa-1 =e.
Если операция коммутативна, то есть ab=ba, то группа называется абелевой или коммутативной.
Примером абелевой группы служит множество целых чисел относительно операции сложения.
Примером не абелевой группы служит группа перестановок Sn n-го порядка относительно операции суперпозиции (умножения перестановок)
В абелевой группе операция обозначается +, нейтральный элемент 0, и обратный к a обозначается –a.
Свойство 2.4 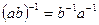 .
.
Доказательство 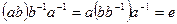 .
.
Подмножество H группы G называется подгруппой, если H является группой относительно операции в G (см. определение подалгебры).
Свойство 2.5. Для того чтобы H являлась подгруппой G необходимо и достаточно, чтобы a*b и a-1 принадлежали H для любых элементов a и b из H.
Доказательство очевидно.
Свойство 2.6. Для того чтобы конечное множество H являлось подгруппой G необходимо и достаточно, чтобы ab принадлежало H для любых элементов a и b из H.
Доказательство. Необходимость очевидна. Покажем достаточность. Для a из H рассмотрим последовательность 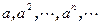 . Поскольку все элементы этой последовательности принадлежат конечному множеству H, то в этой последовательности есть повторяющиеся элементы. Пусть
. Поскольку все элементы этой последовательности принадлежат конечному множеству H, то в этой последовательности есть повторяющиеся элементы. Пусть 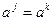 , где j<k. Тогда
, где j<k. Тогда 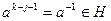 и, значит, выполнены условия предыдущего свойства. Таким образом, H – подгруппа.
и, значит, выполнены условия предыдущего свойства. Таким образом, H – подгруппа.
Изоморфизм групп.
Группа G с операцией * называется изоморфной группе H с операцией o, если существует взаимно однозначное соответствие 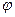 , сохраняющее операции. То есть
, сохраняющее операции. То есть 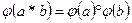 .
.
Например, группа G={0,1} с операцией 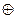 сложение по модулю 2 изоморфна группе H={1,-1} с операцией умножения *.
сложение по модулю 2 изоморфна группе H={1,-1} с операцией умножения *.
Группа называется конечной, если число ее элементов конечно. Число элементов группы называется порядком группы.
Теорема 2.1. Конечная группа порядка n изоморфна некоторой подгруппе симметрической группы n-го порядка.
Доказательство. Перенумеруем элементы группы. Через 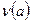 обозначим номер элемента a. Отображение
обозначим номер элемента a. Отображение 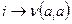 является взаимно однозначным, то есть перестановкой. Действительно, из равенства
является взаимно однозначным, то есть перестановкой. Действительно, из равенства 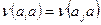 вытекает
вытекает 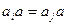 . Умножив последнее равенство справа на
. Умножив последнее равенство справа на 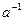 получаем
получаем 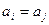 , или i=j. Сопоставим элементу группы a перестановку
, или i=j. Сопоставим элементу группы a перестановку 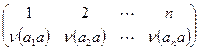 . Указанное соответствие является взаимно однозначным. Действительно, из равенства перестановок
. Указанное соответствие является взаимно однозначным. Действительно, из равенства перестановок 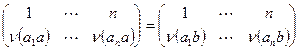 вытекает равенство
вытекает равенство 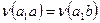 , которое выполняется только если
, которое выполняется только если 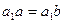 . Умножив полученное равенство слева на
. Умножив полученное равенство слева на 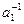 получим a=b. Данное соответствие сохраняет операцию. Поскольку при произведении перестановок
получим a=b. Данное соответствие сохраняет операцию. Поскольку при произведении перестановок 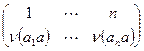 и
и 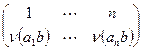 имеем
имеем 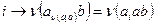 , то
, то 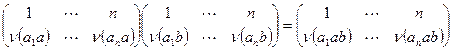 , т.е. отображение сохраняет операцию. Для доказательства теоремы осталось заметить, что множество перестановок вида
, т.е. отображение сохраняет операцию. Для доказательства теоремы осталось заметить, что множество перестановок вида 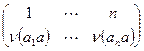 образуют подгруппу в симметрической группе. Действительно, замкнутость по умножению показана выше, а замкнутость при взятии обратного элемента вытекает из равенства
образуют подгруппу в симметрической группе. Действительно, замкнутость по умножению показана выше, а замкнутость при взятии обратного элемента вытекает из равенства 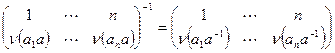 .
.
Из приведенной теоремы вытекают простые факты:
1. С точностью до изоморфизма группа второго порядка единственна
2. С точностью до изоморфизма группа третьего порядка единственна
3. С точностью до изоморфизма существует только две группы четвертого порядка .
При больших n пользоваться данной теоремой затруднительно.
Дата добавления: 2016-07-27; просмотров: 3144;











