Жорданов базис, существование и единственность.

Матрица, имеющая блочно диагональный вид, по главной диагонали которой расположены жордановы клетки, называется жордановой формой. Базис, в котором матрица линейного преобразования имеет жорданову форму называется жордановым.

Следствие 1.7. Для любого линейного преобразования конечномерного векторного пространства над полем комплексных чисел существует жорданов базис.

Доказательство. Базис, построенный при доказательстве предыдущей теоремы, является жордановым. Следовательно, для построения жорданова базиса достаточно линейное пространство расщепить в прямую сумму корневых подпространств и для каждого корневого подпространства найти жорданов базис.

Теорема 1.6. Жорданова форма матрицы единственна, с точностью до перестановок клеток.

Доказательство. Пусть 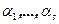- корни характеристического многочлена. Построим жорданов базис. Пронумеруем жордановы клетки. Пусть жорданова клетка с номером i (i=1,…,r) имеет собственное число 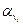и размер 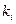. Жордановой клетке в жордановом базисе соответствует цепочка 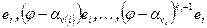. Первый вектор в цепочке имеет высоту 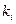, каждый следующий – на единицу меньше предыдущего. Обозначим через 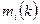количество жордановых клеток с собственным числом 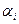порядка k. В корневом подпространстве 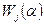содержатся все векторы высоты не большей j, следовательно, 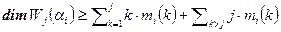. С другой стороны, вектор x из 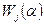раскладывается по тем векторам жорданова базиса, которые соответствуют собственному числу 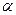и имеют высоту не больше j. Действительно, разложим x по базису. Поскольку пространство разложено в прямую сумму корневых подпространств, то коэффициенты разложения при векторах принадлежащих другим корневым подпространствам равны нулю. Таким образом, 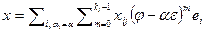. Применим к обеим частям равенства преобразование 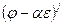, получим 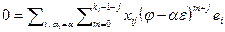. В силу линейной независимости векторов жорданова базиса, все коэффициенты в нем равны 0, и, значит, 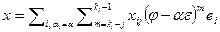. Тем самым установлено равенство 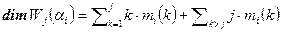. Из полученных равенств выводим 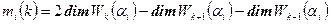при k>1 и 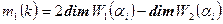. Поскольку размерность корневых подпространств от выбора базиса не зависит, то теорема доказана.