Простота знакопеременной группы
Обозначим через 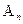 группу четных перестановок порядка n.
группу четных перестановок порядка n.
Лемма 2.1. Если нормальная подгруппа группы 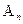 (n>2) содержит цикл из трех элементов, то она совпадает с
(n>2) содержит цикл из трех элементов, то она совпадает с 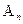 .
.
Доказательство. Не нарушая общности можно считать, что нормальная подгруппа H содержит цикл (1-2-3). Тогда его квадрат (1-3-2) принадлежит H, а также элементы вида 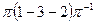 , где
, где 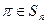 . Положим
. Положим 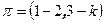 , тогда
, тогда 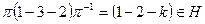 . При
. При 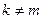 (1-2-k)(1-2-k)(1-2-m)=(1-k-m), следовательно, перестановки вида (1-k-m) принадлежат H. Для попарно не равных друг другу чисел k, m, r (1-k-r)(1-m-k)=(k-r-m), и, значит, все циклы длины 3 принадлежат H. Любая перестановка раскладывается в произведение транспозиций вида (i-i+1), причем в разложении четной перестановки число транспозиций – четное. Рассмотрим произведение двух транспозиций (i-i+1)(j-j+1). Если |i-j|=1, то это произведение – цикл длины 3, и, следовательно, принадлежит H. Если |i-j|>1, то (i-i+1)(j-j+1)=(i-j-j+1)(i-j-i+1) представляется в виде произведения двух циклов длины 3, и также принадлежит H. Таким образом, любая четная перестановка представляется в виде произведения сомножителей из H, и, значит, содержится в H.
(1-2-k)(1-2-k)(1-2-m)=(1-k-m), следовательно, перестановки вида (1-k-m) принадлежат H. Для попарно не равных друг другу чисел k, m, r (1-k-r)(1-m-k)=(k-r-m), и, значит, все циклы длины 3 принадлежат H. Любая перестановка раскладывается в произведение транспозиций вида (i-i+1), причем в разложении четной перестановки число транспозиций – четное. Рассмотрим произведение двух транспозиций (i-i+1)(j-j+1). Если |i-j|=1, то это произведение – цикл длины 3, и, следовательно, принадлежит H. Если |i-j|>1, то (i-i+1)(j-j+1)=(i-j-j+1)(i-j-i+1) представляется в виде произведения двух циклов длины 3, и также принадлежит H. Таким образом, любая четная перестановка представляется в виде произведения сомножителей из H, и, значит, содержится в H.
Теорема 2.11. Группа четных перестановок 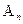 при
при 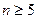 - простая.
- простая.
Доказательство. Допустим в 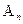 нашлась нормальная подгруппа H. Выберем в H перестановку
нашлась нормальная подгруппа H. Выберем в H перестановку 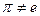 , оставляющую неподвижным как можно большее количество элементов. Запишем перестановку
, оставляющую неподвижным как можно большее количество элементов. Запишем перестановку 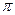 в виде произведения независимых циклов, причем начнем с самого длинного. Рассмотрим случай, когда максимальный цикл имеет длину три и больше
в виде произведения независимых циклов, причем начнем с самого длинного. Рассмотрим случай, когда максимальный цикл имеет длину три и больше 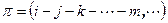 . Перестановка
. Перестановка 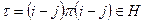 и, значит,
и, значит, 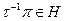 . Поскольку
. Поскольку 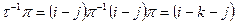 , то
, то 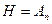 . Рассмотрим случай, когда перестановка
. Рассмотрим случай, когда перестановка 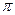 разбивается на независимые циклы длины два общим количеством больше двух. Количество циклов четное. Пусть
разбивается на независимые циклы длины два общим количеством больше двух. Количество циклов четное. Пусть 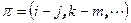 . Так как
. Так как 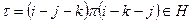 и
и 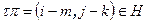 переставляет только 4 элемента, то этот случай противоречит выбору
переставляет только 4 элемента, то этот случай противоречит выбору 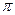 . Осталось рассмотреть единственный случай, когда
. Осталось рассмотреть единственный случай, когда 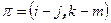 . Пусть r отличен от i, j, k ,m. Перестановка
. Пусть r отличен от i, j, k ,m. Перестановка 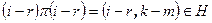 ,
, 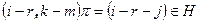 , и по лемме
, и по лемме 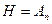 .
.
Дата добавления: 2016-07-27; просмотров: 2445;











