Нормальный делитель, факторгруппа.

Подгруппа H группы G называется нормальным делителем, если для каждого элемента g группы G его левый и правый смежные классы по подгруппе H равны, т.е. gH=Hg.

Теорема 2.5. Подгруппа H группы G является нормальным делителем тогда и только тогда, когда 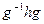содержится в H при любых g из G и h из H.

Доказательство очевидно.

Пусть H – нормальный делитель группы G. На множестве смежных классов введем операцию умножения, индуцируемую групповой операцией. Под произведением смежных классов aH и bH будем понимать множество всевозможных произведений элементов из aH на элементы bH. Поскольку H – нормальный делитель, то все эти произведения содержатся в смежном классе (ab)H. Таким образом, на множестве смежных классов введена операция. Эта операция ассоциативна (aHbH)cH=aH(bHcH), существует нейтральный элемент H, и для каждого элемента aH существует обратный a^-1H. Следовательно, множество смежных классов, относительно введенной операции, образуют группу, которая называется факторгруппой.

Гомоморфизм групп.

Однозначное отображение группы G в группу H, сохраняющее операцию, называется гомоморфизмом группы G в H.

Изоморфизм является частным случаем гомоморфизма.

Свойство 2.9. При гомоморфизме нейтральный элемент группы G отображается в нейтральный элемент группы H.

Доказательство вытекает из равенства .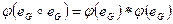

Множество элементов группы G, отображающихся в нейтральный элемент, называют ядром гомоморфизма и обозначают .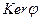

Свойство 2.10.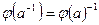

Доказательство. Так как 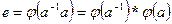, то .

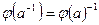Свойство 2.11. Ядро гомоморфизма является нормальным делителем группы G.

Доказательство. Для a из G и b из ядра справедливо 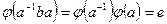, то есть .

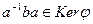Множество элементов группы H, являющиеся образами элементов G, называют множеством образов и обозначают .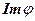

Свойство 2.12. Множество образов 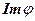является подгруппой H.

Доказательство очевидно.

Теорема 2.6. Факторгруппа 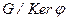изоморфна .

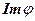Доказательство. Соответствие 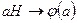является взаимно однозначным и сохраняет операцию, следовательно, оно определяет изоморфизм 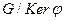и .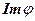

Теорема 2.7. Для любого нормального делителя H группы G существует гомоморфизм, ядро которого равно H. В частности таким гомоморфизмом из G в G/H является .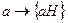

Доказательство очевидно.

Нормальный ряд

Докажем две теоремы о гомоморфизмах.

Теорема 2.8. Пусть H нормальный делитель группы G и P – подгруппа G. Тогда 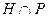- нормальный делитель P и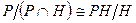

Доказательство. Пусть 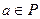и 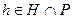. Тогда 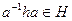так как H нормальный делитель G, и 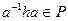т.к все элементы из P. Следовательно, 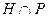- нормальный делитель P. Соответствие 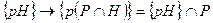является взаимно однозначным и сохраняет операцию. Теорема доказана.

Теорема 2.9. Пусть P – нормальный делитель 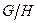и 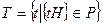. Тогда T – нормальный делитель G и .

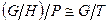Доказательство. Рассмотрим 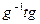, где 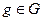, 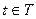. Поскольку 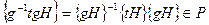, то 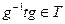, и, значит T – нормальный делитель G. Соответствие 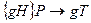является взаимно однозначным, т.к. 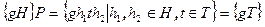и сохраняет операцию.

Группа называется простой, если в ней нет нормального делителя отличного от нее самой и единичной подгруппы.

Нормальный ряд группы – последовательность подгрупп, в которой каждая следующая является нормальным делителем предыдущей. Если все группы нормального ряда 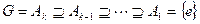содержатся в нормальном ряде 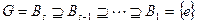, то говорят, что второй нормальный ряд получен уплотнением первого нормального ряда.

Нормальный ряд без повторений, который нельзя уплотнить называется композиционным.

Для нормального ряда 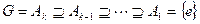определены факторы 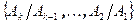. Два нормальных ряда называются изоморфными, если все факторы первого ряда изоморфны факторам второго ряда переставленным в определенном порядке.

Свойство 2.13. Если нормальные ряды 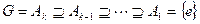и и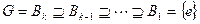зоморфны, то для каждого уплотнения первого ряда можно найти изоморфное ему уплотнение второго ряда.

Доказательство. Допустим, что между подгруппам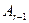и и 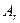появились новые подгруппы 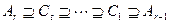. Поскольку 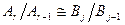и, значит, факторы 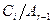изоморфны соответствующим подгруппам 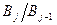. Обозначим через 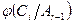соответствующую подгруппу 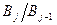. Определим последовательность групп 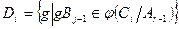, где i=1,…,t. По доказанной выше теореме 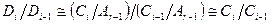. Таким образом, уплотнение второго ряда группами 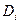является изоморфным. свойство доказано.

Теорема 2.10 (Шрайер) Два нормальных ряда одной группы обладают изоморфными уплотнениями

Доказательство. Пусть 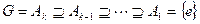- первый нормальный ряд, а 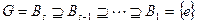- второй нормальный ряд. Если k=2 или s=2, то теорема очевидна. Докажем теорему для k=3 индукцией по s. Рассмотрим случай s=3. Ряды 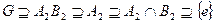и и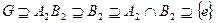зоморфны (т.к. 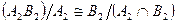и 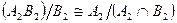) и являются уплотнениями исходных рядов. Пусть утверждение верно для s-1, выведем его справедливость для s. По предположению индукции, ряды 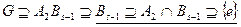и 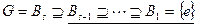обладают изоморфными уплотнениями. Ряд 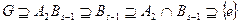изоморфен 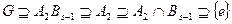, и, значит, для любого уплотнения 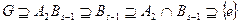найдется изоморфное уплотнение 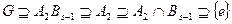. Следовательно, утверждение теоремы при k=3 доказано для всех s. Пусть утверждение теоремы справедливо для k-1, покажем его справедливость для k. 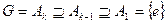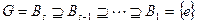Ряды и обладают изоморфными уплотнениями. Пусть 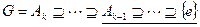- уплотнение первого ряда. По предположению индукции ряды 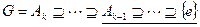и 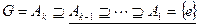обладают изоморфными уплотнениями. Следовательно, теорема доказана.

Следствие 2.5. Любые два композиционные ряда одной и той же группы изоморфны.