Телеграфные уравнения, волновое уравнение
| Рассмотрим распределенную колебательную систему на примере двухпроводной линии. Если расстояние между проводниками мало в сравнении с длиной линии l и длиной волны l, передаваемых колебаний в ней, то векторы магнитного и электрического поля лежат в плоскости, перпендикулярной направлению линии, в этой плоскости удовлетворяют уравнению Лапласа и могут считаться потенциальными. Поэтому для малых участков | 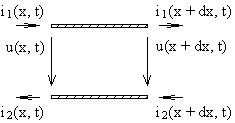 Рис. 79. Двухпроводная линия.
Рис. 79. Двухпроводная линия.
|
линии dx (рис. 79) можно ввести понятия потенциала, тока, распределенных ёмкостей и индуктивностей. Если система не излучает и не взаимодействует с другими проводниками, то в каждом сечении линии токи в обоих проводниках равны по величине и противоположны по направлению: i1(x, t) = -i2(x, t) = i(x, t).
Рассмотрим бесконечно малый элемент dx длины линии, обладающей индуктивностью L и ёмкостью C на единицу длины линии. Для участка dx линии можно записать уравнения Кирхгофа:
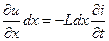 ,
, 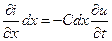 ,
,
откуда легко получаются телеграфные уравнения:
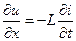 , , 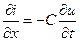 . .
| (9.1) |
Из уравнений (9.1) легко получаются и волновые уравнения для тока и напряжения:
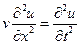 , , 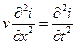 , ,
| (9.2) |
где
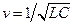 - фазовая скорость. - фазовая скорость.
| (9.3) |
Волновое уравнение можно получить также, если рассматривать, например, распределённую электрическую систему как предельный случай одномерной цепочки, составленной из сосредоточенных индуктивностей и емкостей. Если увеличивать число ячеек на единицу длины цепочки, сохраняя постоянной общую индуктивность и ёмкость, то в пределе система уравнений для цепочки (8.32) перейдёт в волновое уравнение (9.2). Координата x соответствует изменяющемуся номеру ячейки.
Частным решением волнового уравнения (9.2) являются любые функции вида
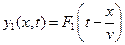 ,
, 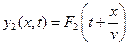 ,
,
соответственно полное решение имеет вид:
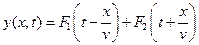 . .
| (9.4) |
Первое слагаемое описывает волну, которая распространяется, не меняя своей формы, в направлении возрастания x, а второе - волну, распространяющуюся с той же скоростью в сторону убывания x. Для процессов, синусоидальных во времени, решение (9.4) принимает форму
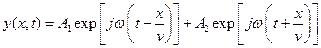 .
.
Здесь величина w(t ± x/v) называется фазой волны, а величина k = w/v - волновым числом. Волновое число характеризует пространственную периодичность волнового процесса, т. е. y(x + nl, t) = y(x, t), и связана с длиной волны соотношением: k = 2p/l.
Для токов и напряжений в линии решение уравнения (9.4) имеет вид:
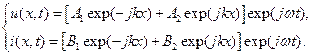
| (9.5) |
Подставляя эти выражения в телеграфное уравнение (9.1), получим связь между коэффициентами:
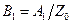 ,
, 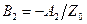 ,
,
где 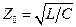 - волновое сопротивление линии. Учитывая связь между коэффициентами, перепишем (9.5) в виде
- волновое сопротивление линии. Учитывая связь между коэффициентами, перепишем (9.5) в виде
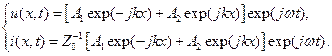
| (9.6) |
Погонные индуктивность и ёмкость линии определяются её геометрией. Для двухпроводной линии в системе СГС получаем
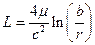 , , 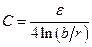 , ,
| (9.7) |
где r - радиус проводов, b - расстояние между ними.
Учитывая два последних соотношения, получим для волнового сопротивления следующее выражение:
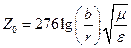 [Ом].
[Ом].
Для коаксиальной линии имеем
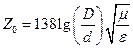 [Ом],
[Ом],
где D и d - диаметры внешнего и внутреннего проводников.
Подставляя погонные L и C в (9.3), получим, что фазовая скорость волны в линии равна
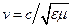 . .
| (9.8) |
Для двухпроводной линии с погонным сопротивлением проводников R и погонной утечкой G между ними телеграфные уравнения (9.1) принимают вид:
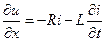 , , 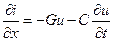 . .
| (9.9) |
Для гармонического во времени процесса уравнения (9.9) запишутся следующим образом:
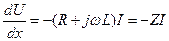 ,
, 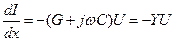 ,
,
где Z и Y - комплексные последовательное сопротивление и параллельная утечка, U и I - комплексные амплитуды напряжения и тока. Из этих двух телеграфных уравнений получим уравнение для U
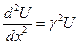 ,
,
где
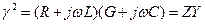 .
.
Его решение имеет вид:
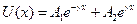 ,
,
причём постоянная распространения g в данном случае является комплексной величиной. Представим её так:
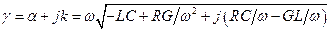 .
.
Тогда мы вправе записать
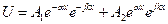 .
.
Теперь и падающая и отражённая волны содержат множитель, характеризующий затухание. Поскольку и мнимая, и действительная части g являются нелинейными функциями частоты, то и фазовая скорость волны v = w/k зависит от частоты. Это явление называется дисперсией. Волновое сопротивление линии с потерями тоже комплекснозначная функция частоты
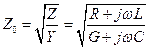 .
.
Дата добавления: 2019-02-08; просмотров: 1040;











