Параметрические системы, соотношения Менли-Роу

Системы с n степенями свободы находят применение в параметрических и автоколебательных устройствах. Параметрическая система с n степенями свободы состоит из нелинейной реактивности и линейной цепи с n контурами, настроенными на комбинационные частоты двух внешних сигналов, действующих на систему. Менли и Роу показали, что между мощностями, выделяющимися в каждом из контуров, существуют определённые соотношения. Эти соотношения позволяют определять максимальные коэффициенты усиления и преобразования сложной параметрической системы.

Рассмотрим поведение нелинейной ёмкости C(u) под действием двух источников напряжения с частотами w₁ и w_н. Как показано в пункте 7.3, в спек­тре тока появятся комбинационные частоты w_ml = mw_н + lw₁ > 0. Запишем за­кон сохранения числа квантов накачки w_н в системе. Если генератор накачки отдаёт в систему мощность P₁₀, то в единицу времени поступает 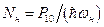квантов накачки. Эти кванты расходуются на образование колебаний с комбинационными частотами. Генератор накачки не является единственным в схеме источником квантов накачки. Дело в том, что при образовании кванта комбинационной частоты w_ml = mw_н + lw₁ > 0 при m < 0 одновременно происходит выделение квантов накачки. Образование одного кванта частоты w_m,l сопровождается поглощением l квантов частоты w₁ и выделением |m| квантов накачки w_н. так как 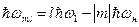. Естественно, что при этом l > |m|w_н/w₁. Полное число квантов накачки, выделяющихся в системе при выделении мощности P_ml < 0 на комбинационной частоте равно 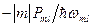. Суммируя по всем возможным m < 0 и по всем возможным l (l > |m|w_н/w₁), а также прибавляя число квантов, приходящих от генератора накачки, получим общее число квантов, выделяющихся в системе:

,

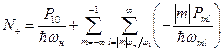(8.52)

Все эти кванты расходуются на образование комбинационных частот с m > 0.

Рассмотрим комбинационное колебание с частотой w_ml = mw_н + lw₁, для которого m > 0. Число l в этом случае может быть любым числом, большим -mw_н/w₁. При образовании одного кванта частоты w_ml затрачивается т квантов накачки, так как 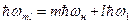. Полное число квантов частоты w_ml, выделяющееся в системе за единицу времени, равно 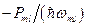. На образование этих квантов в единицу времени затрачивается 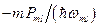квантов накачки. Суммируя по всем m > 0 и l > -mw_н/w₁, по­лучим

.

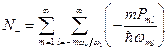(8.53)

Отметим, что в выражении (8.53) необходимо исключить слагаемое с m = 1 и l = 0, так как оно уже вошло в формулу (8.52) как 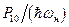. Закон сохранения чис­ла квантов накачки теперь принимает вид:

.

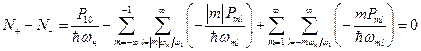Сменив знаки у индекса суммирования во втором слагаемом, включив слагаемое 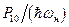в сумму как член с m = 1 и l = 0, и умножив всю сумму на 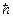, получим первое соотношение Менли-Роу:

.

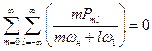(8.54)

Здесь добавлено нулевое слагаемое с m = 0.

Аналогичным образом можно получить и второе соотношение Менли-Роу, представляющее собой закон сохранения квантов сигнала

.

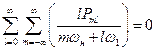(8.55)

Отметим, что оба соотношения Менли-Роу получены в предположении, что реактивный нелинейный элемент не имеет потерь.

В каждое из соотношений Менли-Роу входят члены, соответствующие всем частотам схемы, но в (8.54) отрицательными явля­ются частоты с m < 0, а в соотношении (8.55) - с l < 0, поэтому формально в этих соотношениях все суммы можно писать от -¥ до ¥, так как P_ml = P_(-m)(-l).

Из соотношений Менли-Роу (8.54) и (8.55) следует, что независимо от вида нелинейности и нагрузки распределение мощности по комбинационным частотам определяется только величиной и знаками комбинационных частот.

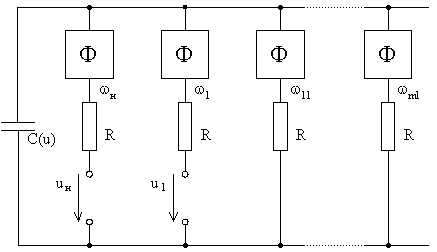Рис. 78. Параметрический усилитель.

Пусть система с п степенями свободы состоит из идеальных фильтров Ф, настроенных на все возможные комбинационные частоты, и одинаковых сопро­тивлений R, а к фильтрам, настроенным на частоты w₁ и w_н, подключены, соот­ветственно, источники сигнала и накачки (рис. 78). Простейший пример - ре­генеративный усилитель с одним дополнительным контуром, настроенным на частоту w_н - w₁. Тогда в соотношения Менли-Роу войдут три мощности: P₁₀ - мощность накачки, P₀₁ - мощность сигнала и P_1(-1) - мощность, выделяемая в дополнительном контуре:

,  .

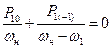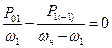(8.56)

Естественно, что поступающая от генератора накачки мощность положительна, т. е. P₁₀ > 0. Тогда из (8.56) следует, что

,  ,  .

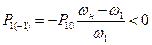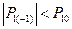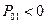Эти неравенства показывают, что только часть мощности накачки поступает в дополнительный контур. Остальная часть, как видно из (8.56), идет в источник сигнала (P₀₁ < 0), т. е. расходуется на его усиление. Система представляет собой регенера­тивный усилитель, охваченный положительной обратной связью, склонный к самовозбуждению и имеющий значительные шумы.

Нерегенеративный усилитель получается, если дополнительный контур настроен на частоту w_н + w₁ (преобразование вверх). Поэтому в соотношения Менли-Роу (8.54) и (8.55) будут входить мощности P₁₀, P₀₁ и мощность, рассеиваемая в дополнительном контуре P₁₁. Эти соотношения примут вид:

,  .

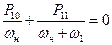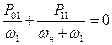(8.57)

Из цепи накачки в систему поступает мощность P₁₀ > 0. Тогда из (8.57) следует, что P₁₁ = -P₁₀(w_н + w₁)/w_н < 0, P₀₁ = -P₁₁w₁/(w_н + w₁) > 0.

Это озна­чает, что на управление нелинейной емкостью расходуется энергия как от источника накачки, так и от источника сигнала. В таком случае схема не способна к самовоз­буждению. Максимальное усиление по мощности такого усилителя - преобразователя частоты - равен

,

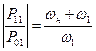(8.58)

что согласуется с оценкой (7.30), если положить w₂ = w_н + w₁.