Вынужденные колебания в распределённых системах
По аналогии с вынужденными колебаниями в системах с многими степенями свободы удобно раскладывать и вынуждающую силу, и вынужденные колебания по собственным функциям системы. Если частота внешней силы совпадает с одной из собственных частот системы, то происходит резонансное увеличение амплитуды колебаний.
Рассмотрим разомкнутую на концах двухпроводную линию с потерями, в которой действует распределённая внешняя сила. Подставляя в первое уравнение системы (9.9) 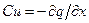 ,
, 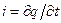 , получим
, получим
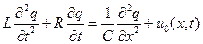 , ,
| (9.16) |
где L, C, R - постоянные погонные параметры линии.
Пусть линия разомкнута на обоих концах, т. е. q(0, t) = q(l, t) = 0. Разложим внешнюю силу в ряд на интервале 0 £ x £ l по собственным функциям вида (9.14) разомкнутой на концах линии
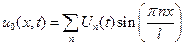 , ,
| (9.17) |
а коэффициенты разложения найдём, используя условие (9.15) ортогональности собственных функций:
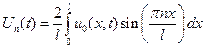 . .
| (9.18) |
Естественно искать решение уравнения (9.16) также в виде ряда по собственным функциям линии с разомкнутыми концами
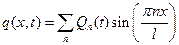 . .
| (9.19) |
Подставим (9.17) и (9.19) в исходное уравнение (9.16):
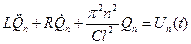 , n = 1, 2, … , n = 1, 2, …
| (9.20) |
Получилась бесконечная система обыкновенных ДУ относительно Qn(t). Каждое из них имеет обычный вид колебательного уравнения для системы с одной степенью свободы, на которую действует внешняя сила Un(t). Уравнения независимы, и поэтому Qn(t) можно рассматривать как нормальные координаты системы. Число таких координат бесконечно. Если отсутствует какая-либо компонента внешней силы Un(t), то соответствующая координата Qn(t) совершает только свободное затухающее колебание.
Решение уравнений (9.20) может быть записано через интеграл Дюамеля:
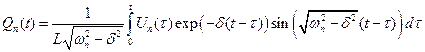 . .
| (9.21) |
Здесь обозначено: 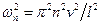 ,
, 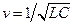 ,
, 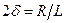 .
.
Для гармонического синхронного и синфазного внешнего воздействия Un(t) = Un0exp(jw0t) в установившемся режиме при t >> 1/d получаем
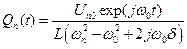 .
.
Суммируя по всем n, получим общее решение уравнения (9.20) в виде
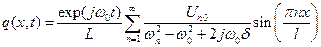 . .
| (9.22) |
Если частота внешнего воздействия w0 совпадает с одной из собственных частот системы wn, то наблюдается резонансное увеличение амплитуды.
В частном случае, если гармоническое внешнее воздействие приложено в одной точке x = b, получаем:
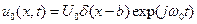 ,
,
где d(x) - дельта-функция. Определим коэффициенты разложения функции u0(x, t)
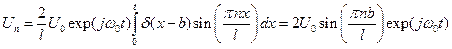 .
.
Общее решение в этом случае будет иметь вид
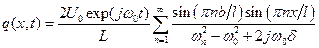 . .
| (9.23) |
Нетрудно видеть, что если b = l/n, т. е. внешняя сила приложена к узлу, то q(x, t). Это явление аналогично ортогональности вынуждающей силы на одной из собственных частот системы и собственного колебания на этой частоте для системы с многими степенями свободы.
Дата добавления: 2019-02-08; просмотров: 743;











