Предварительное вычисления
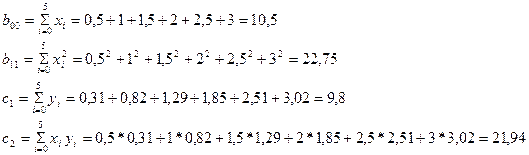
и следовательно
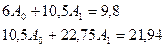
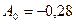
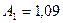
Искомый многочлен y=1,09x-0,28
Лекция 18
Задачи на собственные значения
Основные понятия
Большое число научно-технических задач, а также некоторые исследования в области вычислительной математики требует нахождения собственных значений и собственных векторов матриц.
Введем некоторые определения для изложения материала данного параграфа.
Рассмотрим квадратную матрицу n-го порядка.
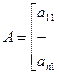
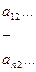
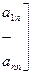
Рассмотрим систему Ax=hx (1)
Когда система (1) имеет не нулевое решение 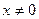
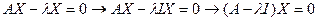 (1)
(1)
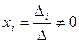 тогда
тогда 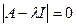 (2)
(2)
или
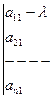
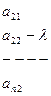
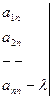 =0 (2)
=0 (2)
Выражение (2) называется характеристическим или весовым полиномом относительно h
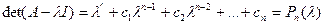
Корни этого многочлена 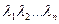 являются собственными значениями матрицы А.
являются собственными значениями матрицы А.
Они характеризуются тем свойством, что дают нетривиальные решение системы(1) 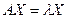 . Чтобы было нетривиальное решение
. Чтобы было нетривиальное решение 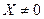 необходимо и достаточно
необходимо и достаточно 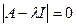 (2) Действительно, если вместо
(2) Действительно, если вместо 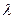 стоит один из корней собственного полинома
стоит один из корней собственного полинома 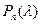 , то выражение (2) обращается в 0. И для этого
, то выражение (2) обращается в 0. И для этого 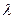 существует ненулевое решение системы (1). Это решение и является собственным вектором. Поиск собственных значений и собственных векторов матрицы A является основной задачей теории устойчивости, надежности и т.п. Существует много методов нахождения собственных векторов и собственных значений матрицы А.
существует ненулевое решение системы (1). Это решение и является собственным вектором. Поиск собственных значений и собственных векторов матрицы A является основной задачей теории устойчивости, надежности и т.п. Существует много методов нахождения собственных векторов и собственных значений матрицы А.
Рассмотрим некоторые из них.
Пример
Вычислить собственные числа и собственные векторы матрицы 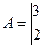
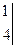
Решение. Составим характеристический многочлен 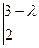
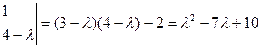
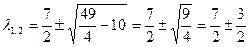
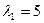
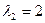
Для нахождения собственных векторов 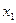 и
и 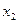 соответствующих значениям
соответствующих значениям 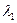 и
и 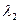 Составим системы уравнений типа
Составим системы уравнений типа 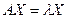 для каждого из них при
для каждого из них при 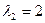
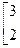
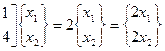
Или запишем в виде системы уравнений
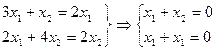
Эти уравнения линей зависимы (даже совпадают) поэтому оставим одно из них.
Полагаем 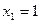
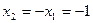 и собственный вектор соответствующий числу
и собственный вектор соответствующий числу 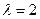 имеет вид
имеет вид 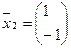 или,
или, 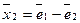 , где
, где 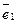 и
и 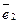 единичные орты выбранной системы координат.
единичные орты выбранной системы координат.
Аналогично находим первый собственный вектор, соответствующий собственному числу 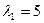
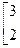
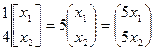
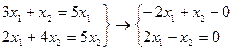
Отсюда 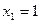
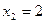
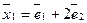
Вектор 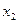 нормирован, нормируемый вектор
нормирован, нормируемый вектор 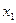 , разделив его компоненты на наибольшую из них получим
, разделив его компоненты на наибольшую из них получим 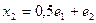
Можно даже привести векторы к единичной длине разделив его компоненты на значения модулей векторов.
В этом случае 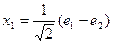
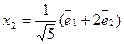
Дата добавления: 2016-07-27; просмотров: 1843;











