Алгоритм вычисления суммы бесконечного ряда
Характерным примером итерационных циклов является задача вычисления суммы бесконечного ряда:
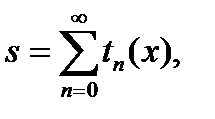
где tn(x) – слагаемое, зависящее от параметра x (в общем случае) и номера n. Вычисляемая последовательность
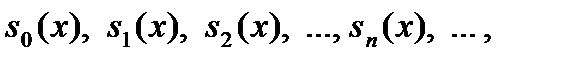
где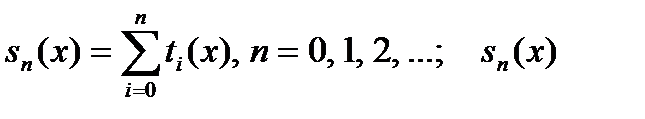 
– частная сумма.
Для контроля погрешности можно использовать последовательность
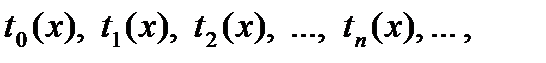
где tn(x) = sn(x) – sn-1(x) – слагаемые ряда n.
.
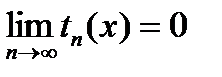Условие выхода из итерационного цикла (справедливо при знакопеременном ряде {tn(x)}):
| tn ( x ) | < e .
Алгоритм вычисления бесконечной суммы является модификацией одного из алгоритмов вычисления конечной суммы. Если применение рекуррентных формул нецелесообразно, то вычисления будут наиболее эффективными, если каждое слагаемое определять по общей формуле и полученные значения накапливать в некоторой переменной. Общий вид схемы алгоритма, реализующего вычисление бесконечной суммы с погрешностью e с помощью цикла с предусловием, показан на рис. 5.10, а.
Если для вычисления слагаемых используются рекуррентные соотношения
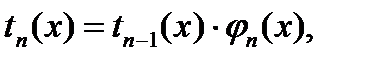
то общая схема итерационного алгоритма для вычисления бесконечной суммы показана на рис. 5.10, б.
Например, тригонометрическая функция sin(x) может быть представлена в виде бесконечной суммы
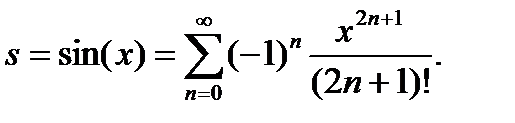
В данном случае
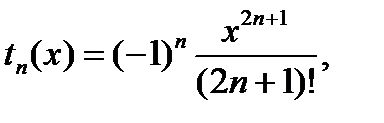
тогда
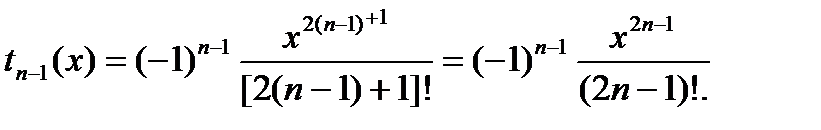
Теперь можно определить
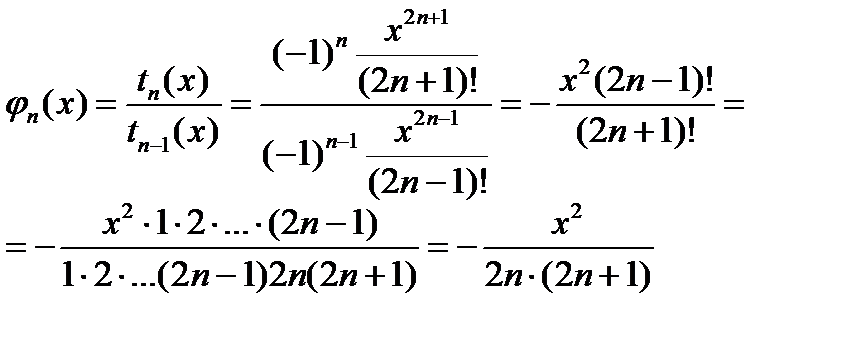
Начальное значение слагаемого находим по формуле
| Начало |
| Ввод x, ε |
|
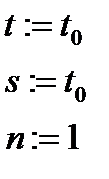
| |t|>ε |
| t:=tn(x) s:=s+t n:=n+1 |
| Конец |
| Вывод s |
| Начало |
| Ввод x, ε |
|
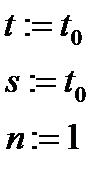
| |t|>ε |
| t:=tφn(x) s:=s+t n:=n+1 |
| Вывод s |
| Конец |
| Нет |
| Да |
| Нет |
| Да |
| Рис. 5.10 Схемы алгоритмов итерационных циклов, реализующих вычисление бесконечной суммы |
| б) |
| а) |
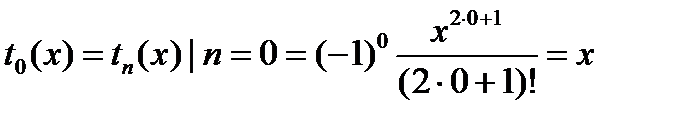
Дата добавления: 2016-05-31; просмотров: 2575;