Нахождение наибольшего по модулю собственного значения матрицы А.

Пусть имеется характеристический определитель 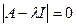или

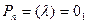
Корни этого полинома 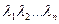является собственными значениями матрицы А, причем пусть

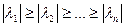(1)

Укажем приближенный метод нахождения 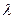. Возьмем произвольный вектор 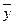и разложим по собственным векторам 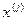матрицы А.

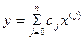,где 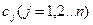- постоянные коэффициенты

Проведя преобразование А над вектором 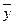получим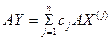

Отсюда, т.к. вектор 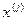собственный вектор преобразования А, т.е. 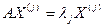получим

AУ- называется итерацией вектора 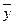Последовательно образуя итерации 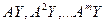, получим 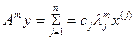(2) (м-итераций)

Выберем в пространстве 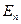базис 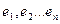(не обязательно единичный).

Пусть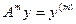

Координаты вектора 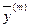в выбранном базисе .

Разлагая собственные векторы 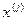по векторам выбранного базиса 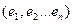получим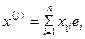

Отсюда подставляя (3) в (2) получим (3)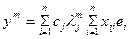

Или меняя порядок суммирования получим 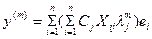(4)

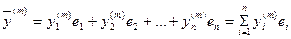Но (4а)

Приравнивая (4) и (4а) получим

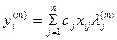(5)

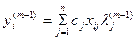(6)

Разделив (6) на (5) получим

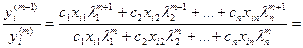
Пусть 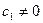и 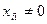, тогда

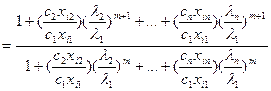
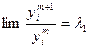с учётом неравенства (1)

Литература.

1. Волков Е.А. Численные методы.

2. Турчак Л.И. Основы числительных методов.

3. Демидович Б.И. и Марон И.А. Основы вычислительной математики.

4. Копченова И.В. и Марон И.А. Вычислительная математика в примерах и задачах.

5. Перумов У.Г. Числительные методы

Высшее образование Москва 2004г.