Алгоритм вычисления ПХ классическим методом
По определению, переходной характеристикой цепи h1(t) является её выходной сигнал при единичной ступенчатой функции на входе u1(t)=σ1(t), описываемой выражением
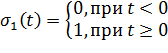
| (6.1) |
и диаграмма которой представлена на рисунке Рисунок 6.1.
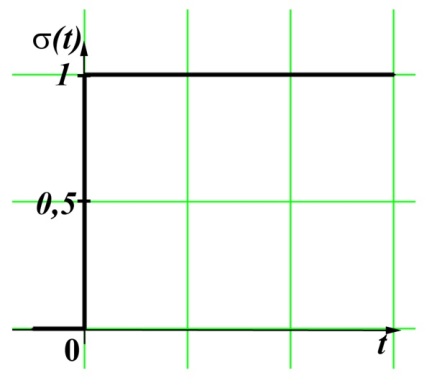
Рисунок 6.1 – Единичная ступенчатая функция
Ниже приведён алгоритм вычисления ПХ классическим методом. Для примера рассчитаем ПХ цепи второго порядка рисунка Рисунок 6.2.
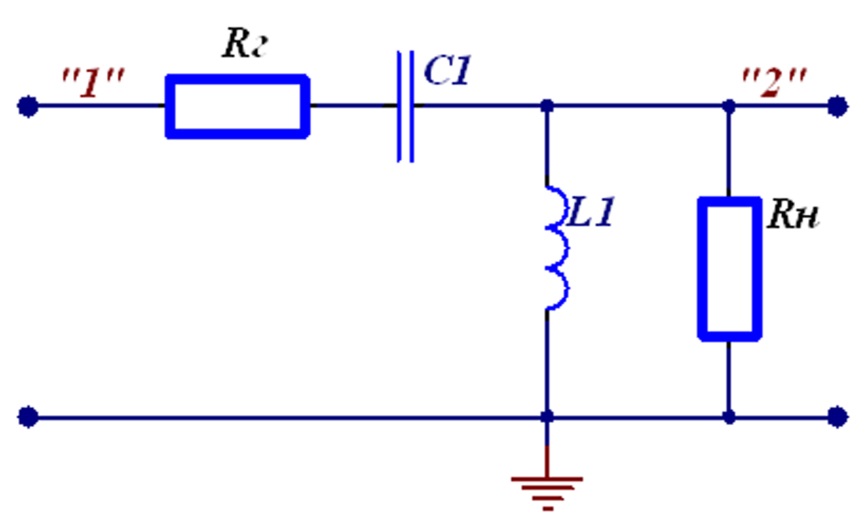
Рисунок 6.2
a) Определение установившейся составляющей. Выражение переходной функции состоит из свободной составляющей и установившейся
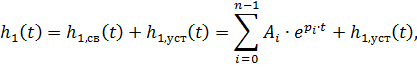
| (6.2) |
где n – порядок цепи,
pi – собственные частоты цепи,
Ai – постоянные интегрирования.
Для определения установившейся составляющей в после коммутационной цепи постоянного тока конденсаторы заменяем обрывом, катушки – коротким замыканием. После преобразований цепь придёт к виду рисунка Рисунок 6.3.
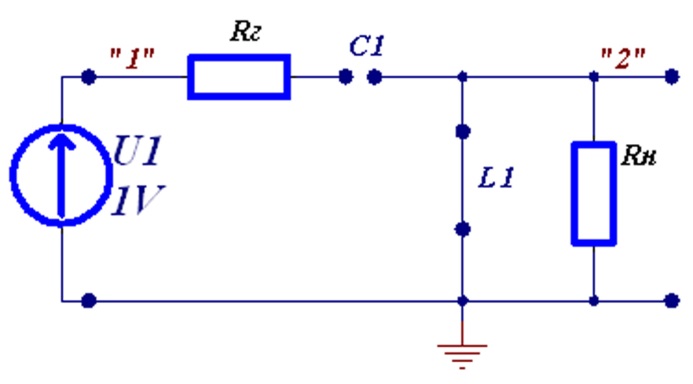
Рисунок 6.3 – Схема в установившемся режиме при постоянном источнике U1
Очевидно, что выходное напряжение U2уст=0 из-за короткого замыкания выходных точек и отсутствия тока через обрыв. Таким образом
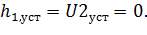
| (6.3) |
b) Формирование характеристического полинома D(p), определение собственных частот. Сформировать характеристический полином вы можете следующими способами:
- из выражения для входного операторного сопротивления Z(p), если на входе – источник напряжения, либо из выражения для входной операторной проводимости Y(p), если на входе – источник тока;
- из выражения для главного определителя операторной системы уравнений состояния, составленной любым из методов анализа – на основе законов Кирхгоффа, методом контурных током или узловых потенциалов;
- из выражения знаменателя передаточной функции H(p).
В настоящей курсовой работе передаточная функция является одним из результатов решения задач раздела 4 и выражением его знаменателя можно воспользоваться для определения собственных частот. Передаточная функция для схемы рисунка 6.2 получена в приложении A (выражение A.7)
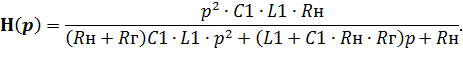
| (6.4) |
Составим из выражения знаменателя характеристический полином
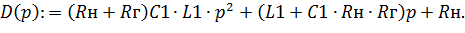
| (6.5) |
Корни уравнения
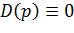
| (6.6) |
являются собственными частотами. В программе MathCad решить уравнение (6.6) автор предлагает следующими приёмами:
Приём 1 – с помощью команды «Symbolics»→ «Variable» → «Solve» главного меню:
- в введённом характеристическом полиноме (6.4) в любом месте выделяет искомая переменная «p» (рисунок 6.4);
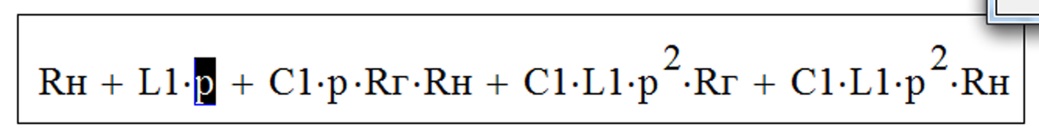
Рисунок 6.4
- выполняется команда «Symbolics»→ «Variable» → «Solve» (рисунок 6.5);
- для анализа численных значений после полученного символьного результата поставим знак «=» (рисунок 6.6);

Рисунок 6.5

Рисунок 6.6
- полученный вектор численных результатов копируете в буфер памяти (весь вектор со скобками) и присваиваете вектору p (рисунок 6.7).
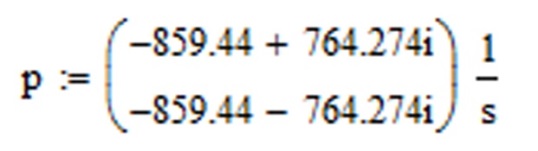
Рисунок 6.7
Результаты получены при
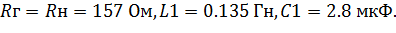
| (6.7) |
Приём 2 – определение собственных частот помощью оператора «Solve» панели «Symbolics»:
- вводим в программу MathCad функцию (6.5);
- на панели «Symbolics» выбираем оператор «Solve» (рисунок 6.8);
- на месте «кирпичика» оператора «Solve» вписываем наименование функции характеристического полинома (рисунок 6.9);
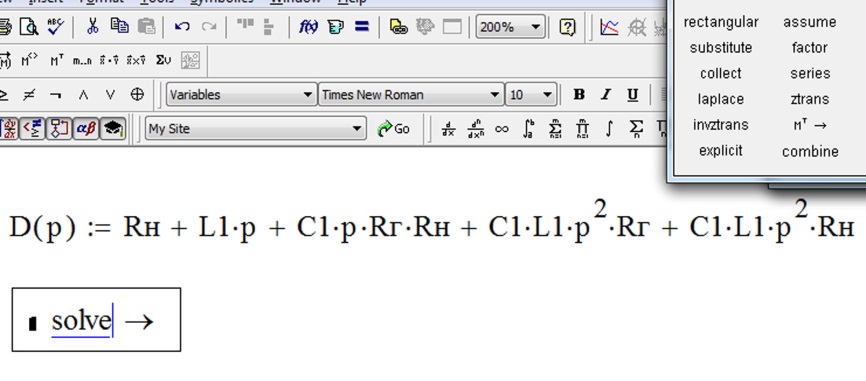
Рисунок 6.8

Рисунок 6.9
- если получился «кривой», неудобочитаемый результат, аналогичный рисунку 6.9, после результата можно поставить знак «=» (рисунок 6.10);

Рисунок 6.10
- полученный вектор численных результатов присваиваете вектору собственных частот p (рисунок 6.7).
Количество корней должно соответствовать количеству реактивных элементов цепи или порядку характеристического полинома. Сами корни могут быть:
- чисто вещественными, отрицательными;
- если порядок цепи – 2 или больше, то среди корней могут встречаться пары комплексно сопряжённых частот вида
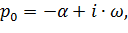
| (6.8) |
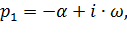
| (6.9) |
причём их вещественные части – обязательно отрицательные. В выражениях корней (6.8) и (6.9) параметр α – декремент затухания цепи, ω – циклическая частота затухающих гармонических колебаний ПХ. В рассматриваемом примере собственные частоты – комплексно сопряжённые, значения параметров следующие
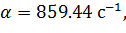
| (6.10) |
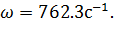
| (6.11) |
c) Определение независимых начальных условий. Независимые начальные условия – значения напряжений конденсаторов и токов катушек до коммутации, в случае вычисления ПХ – до скачка напряжения на входе. Так как до скачка напряжение на входе нулевое, то все независимые начальные условия – нулевые:
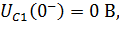
| (6.12) |
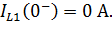
| (6.13) |
d) Определение зависимых начальных условий. Зависимыми начальными условиями являются:
- значение искомой электрической величины, если эта величина – не ток катушки и не напряжение конденсатора;
- значения производных искомой величины от первого до n-1-го порядка, где n – порядок цепи. Для схемы рассматриваемого примера рисунка 6.2 n=2.
Для определения начального значения самой электрической величины схема преобразуется для момента времени t=0+, непосредственно следующим за коммутацией, при этом:
- конденсаторы заменяются источниками напряжения, ЭДС которых равны напряжениям конденсаторов до коммутации 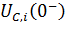 ;
;
- если какое либо напряжение 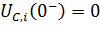 , соответствующий конденсатор можно заменить не источником напряжения, а коротким замыканием (КЗ);
, соответствующий конденсатор можно заменить не источником напряжения, а коротким замыканием (КЗ);
- индуктивности заменяются источниками тока, номиналы которых равны соответствующим токам катушек до коммутации 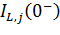 ;
;
- если какой либо ток 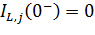 , соответствующую катушку можно заменить не источником тока, а обрывом;
, соответствующую катушку можно заменить не источником тока, а обрывом;
- источники энергии представляются постоянными источниками, значения ЭДС которых определяются значениями их функций при t=0+ – Ek(0+) и Jm(0+). Значения можно определить по графикам или с помощью заданных выражений.
Так как в рассматриваемом примере все независимые начальные условия - нулевые, то для момента t=0+ схема преобразуется к виду рисунка 6.11. Расчёт следующий:
- вычислим сперва ток
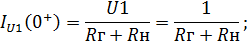
| (6.14) |
- а затем напряжение 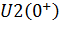
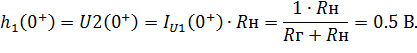
| (6.15) |
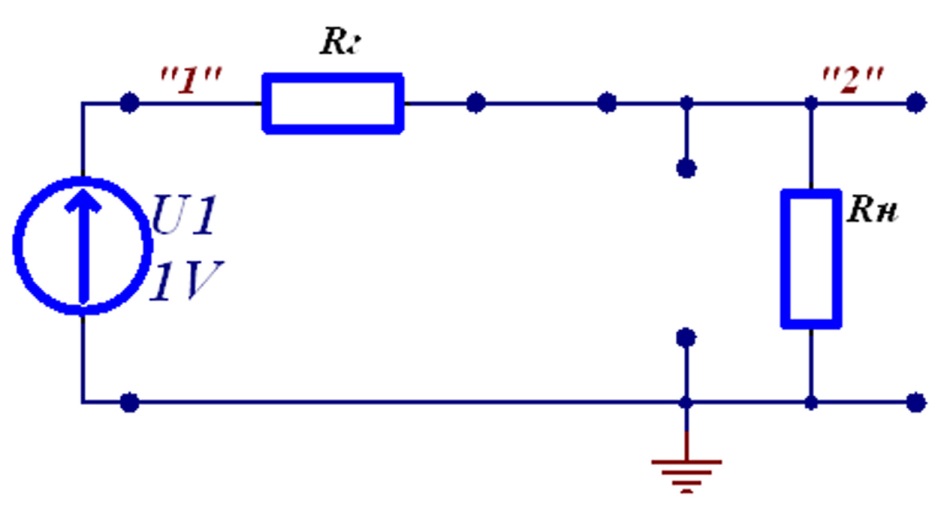
Рисунок 6.11 – Схема при t=0+
Порядок рассматриваемой цепи n=2, поэтому необходимо определить ещё начальное значение первой производной 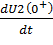 . Для этого, используя законы Ома и Кирхгоффа, необходимо выразить искомую величину U2 через токи катушек, токи источников тока, напряжения конденсаторов, напряжения источников напряжения.
. Для этого, используя законы Ома и Кирхгоффа, необходимо выразить искомую величину U2 через токи катушек, токи источников тока, напряжения конденсаторов, напряжения источников напряжения.
Для рассматриваемой схемы (рисунки 6.2, 6.12) выполним это следующим образом:
- по второму закону Кирхгоффа
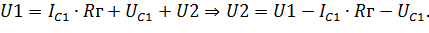
| (6.16) |
В полученном выражении IC1 – ни ток катушки, ни ток источника тока;
- по первому закону Кирхгоффа
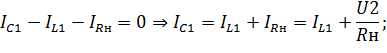
| (6.17) |
- выражение для 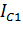 (6.16) подставим в (6.15)
(6.16) подставим в (6.15)
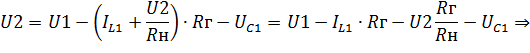
| |
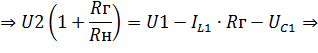
| |
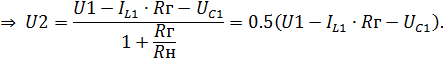
| (6.18) |

Рисунок 6.12
Из соотношений между токами и напряжениями для конденсаторов и катушек
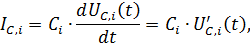
| (6.19) |
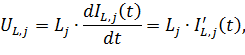
| (6.20) |
следуют выражения для производных
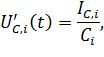
| (6.21) |
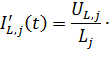
| (6.22) |
Продифференцируем обе части выражения (6.18)
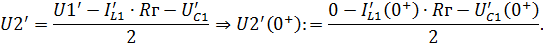
| (6.23) |
Для определения значений 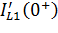 и
и 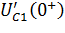 определим
определим 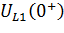 и
и 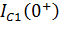 по схеме рисунка 6.11:
по схеме рисунка 6.11:
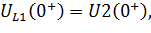
| (6.24) |
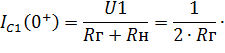
| (6.25) |
Отсюда
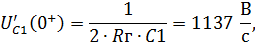
| (6.26) |
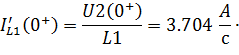
| (6.27) |
Введя (6.26), (6.27), а затем (6.23) в программу MathCad, вычислим начальную производную
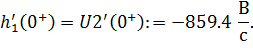
| (6.28) |
e) Для вычисления постоянных интегрирования Ai – коэффициентов перед экспонентами в выражении (6.1) решается система линейных уравнений
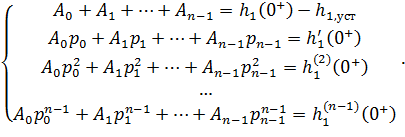
| (6.29) |
Для рассматриваемой схемы система (6.29) примет вид
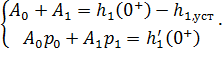
| (6.30) |
Вводим в MathCad матрицу коэффициентов и вектор правых частей
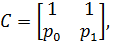 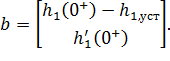
| (6.31) |
Решим систему в программе MathCad c помощью обратной матрицы
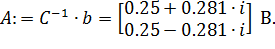
| (6.32) |
f) Ввод функции ПХ и построение диаграммы в программе MathCad.
- Если все полученные собственные частоты – вещественные, то в программе MathCad функция ПХ вводится в виде, аналогичном (6.1).
- Если среди собственных частот присутствует пара комплексно сопряжённых
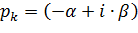 и и 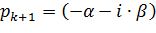 , ,
| (6.33) |
то им в выражении ПХ будет соответствовать сумма экспонент
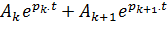 , ,
| (6.34) |
в которой 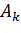 и
и 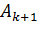 комплексно сопряжены. Сумма (6.34) заменяется выражением
комплексно сопряжены. Сумма (6.34) заменяется выражением
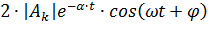 , ,
| (6.35) |
В котором 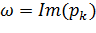 ,.
,.
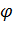 – аргумент либо коэффициента
– аргумент либо коэффициента 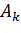 , либо
, либо 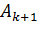 . Выбор должен оставаться за тем из коэффициентов, который соответствует собственной частоте с положительной мнимой частью. Для варианта (6.31)
. Выбор должен оставаться за тем из коэффициентов, который соответствует собственной частоте с положительной мнимой частью. Для варианта (6.31) 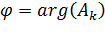
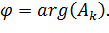
| (6.36) |
Для рассматриваемой схемы рисунка (6.12) все собственные частоты являются комплексно-сопряжёнными, поэтому выражение ПХ для схемы примет вид
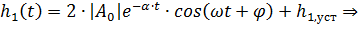
| |
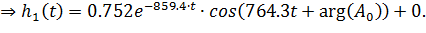
| (6.37) |
Дата добавления: 2016-12-27; просмотров: 2301;











