Абсолютная величина и норма матрицы.

Под нормой матрицы A~(a_ij) понимают действительное число 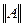, удовлетворяющее следующим условиям:

1) 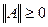( 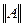=0 тогда и только тогда, когда A=0)

2) 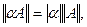где α- число.

3)

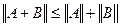
4)

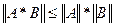
Матрица определяется тремя нормами.

1)

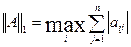
2)

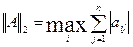
3)

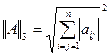
Для матрицы

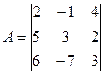
Найти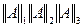

Решение

1)

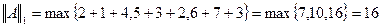
2)

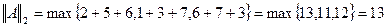
3)

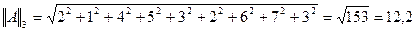
Для вектора 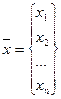эти нормы вычисляются по следующим формулам

1) 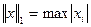-максимальная из координат вектора взятая по модулю

2) 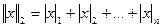- сумма модулей координат вектора

3) 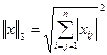-корень квадратный из суммы квадратов модулей координат вектора

Пример.

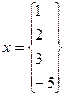
Вычислить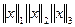

Решение

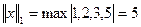
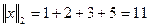
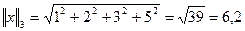
Метод простой итерации.

Пусть задана система линейных уравнений

Ax=b=>Ax-b=0 (1) Ax`-b=ξ- невязка

x- x+ Ax-b=0=>x= (I-A) x+ b=>x=Bx+ b (2)

Пусть матрица B невырожденная, т.е. det B≠0/

Выбрав произвольно x₀ вычисляем последовательно x_k

x_k= Bx_k-1+b (3)

Пусть x^*- точное решение уравнения (1) и (2), тогда

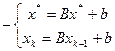
(x_k-x^*) =B (x_k-1-x^*) (4)

(x_k-x^*) =B (x_k-1-x^*) = B B (x_k-2-x^*) = B^k (x₀-x^*) (4a)

Пронормируем последнее выражение (4а) получим:

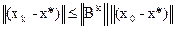(5)

Из полученного неравенства следует, что при произвольном выборе x₀ соотношение 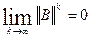(6) при 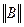< 1 (7)

Эквивалентно 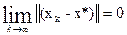или 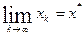. Соотношение (6) возможно, если выполнено неравенство (7). 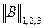< 1